凸函数

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第68页（4612字）

凸函数是一类具有良好性质的重要函数，在数学的众多领域中都具有广泛应用，在现代变分学、最优化理论、最优控制、数理经济学和非线性泛函分析等学科中发挥着重要作用，20世纪60年代中后期形成的以凸函数和凸集为基本研究对象的新兴数学分支－凸分析，已成为上述有些学科的重要理论基础和有力工具。

19世纪末20世纪初，哈代(O．Holder)、颜森(J．L．W．V．Jensen)和闵可夫斯基(H．Minkowski)奠定了凸函数理论的基础，闵可夫斯基1892年曾提出凸函数的概念。设是一凸集(即对任意x，，λ∈［0，1］有，f_：C→R，如果对任意，λ∈(0，1)有

f(λx+(1－λ)y)≤λf(x)+(1－λ)f(y)

则称f是C上的凸函数，如果当x≠y时，严格不等式成立，则称f是C上的严格凸函数。从几何观点来看凸函数是很直观的：如果f(x)的图象上任意两点连成的弦位于所对应的曲线上或曲线上方，那么实值函数f便是凸函数。上述定义等价于：对任意x₁、x₂、…，，对任意λ₁，λ₂，…，λ_k∈［0，1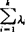］，，有

在凸函数发展初期，人们就发现，利用函数的凸性可以简便地证明一些重要不等式，例如，由的凸性可得不等式：

其中

在上述不等式中令，再以代替x_．(i=1，2，…，n)可得

这就是算术－几何－调和平均不等式。

凸函数理论真正引起重视，是由于20世纪40年代后期和50年代初期冯·诺伊曼(J．Von Neumann)、但泽(G．Dantzig)、库恩(H．W．Kuhn)和塔克(A．W．Tucker)等人对博弈论和数学规划的研究。50年代初，人们对凸函数、凸集和凸锥进行了深入研究，这方面的代表人物是芬凯尔(W．Fenchel)和克利(V．L．Klee)，他们的研究为后来凸分析的形成打下了扎实基础。

设f是定义在上的函数，称

epif=｛(x，α)∈Rⁿ⁺¹｜x∈C，α∈R，f(x)≤α｝

为f的上图，f的凸性与集合epi f的凸性紧密相关，即有

命题1 f是凸集上的凸函数当且仅当f的上图epi f是Rⁿ⁺¹中的凸集。

凸函数在其定义域中不一定处处连续或可微，不过在其定义域的内点处一定连续，且在内点处沿任何方向的左、右方向导数都存在，对一元函数还有

命题2 设f为(a，b)上的实值函数，那么f在(a，b)上凸的充要条件是f在(a，b)上的左导数f_－和右导数f₊处处存在，且对x₁、x₂∈(a，b)，x₁＜x₂，有

一般函数可微未必一阶偏导数连续，而芬凯尔1951年证明

命题3 开凸集上的实值可微凸函数必有连续的一阶(偏)导数。

对二次可微函数，拉达玛赫(H．Rademacher)1922年证明

命题4 设f是开凸集上的二次可微函数，则f是C上的凸函数的充要条件是：f的Hessian矩阵在C上处处都是半正定的，即对每个x∈C，有

y^T▽²f(x)y≥0，。

凸函数漂亮的极值性质在最优化理论中起着重要作用。

命题5 凸集上的凸函数的任一局部极小值点一定是整体极小值点。

命题6 开凸集上的可微凸函数的极小值点与驻点等价。

凸函数的现代发展和强大威力是和凸分析的形成联系在一起的。凸分析正式成为一门数学分科是以法国的莫罗(J．J．Moreau)1966年的讲义《凸泛函》和美国的洛克菲勒(R．T．Rockafellar)1970年的着作《凸分析》的问世为标志的。这两位数学家对凸函数的性质进行了深入系统研究，把导数(梯度)的概念对凸函数进行推广，提出了次微分(subdifferential)的概念。设C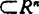是非空凸集，f：C→R是凸函数，向量ξ∈Rⁿ称为f在x∈C的次梯度，如果对一切y∈C，均成立

f(y)≥f(x)+ξ^T(y-x)

这个不等式有一个简单的几何意义：仿射函数h(y)=f(x)+ξ^T(y-x)的图象是上图epi f在(x，f(x))点的非垂直支撑超平面。

凸函数f在x的所有次梯度的集合称作f在x的次微分，记作。可能是空集、可能只包含一个向量，也可能包含无穷多个向量。

如果不是空集，则称f在x是次可微的。凸函数在其定义域的内点总是次可微的，反过来，设f是定义在非空凸集C上的实值函数，如果f在C的任一内点处次可微，则f在C的内部是凸的。因此，Rⁿ上的实值函数是凸函数的充分必要条件为处处存在次梯度，这一点是M．S．Bazaraa和C．M．Shetty在1976和1979年出版的两本书中明确指出的，它反映了函数的凸性与次可微性的密切关系。

凸函数f在x可微的充要条件是：(x)恰好只含单个向量ξ，并且，这时ξ=▽f(x)。

次梯度的特性可以用方向导数来表征，即有

其中是f在x点沿方向h的右方向导数。

莫罗和洛克菲勒发现了次微分的一些很好的性质，如：

(1)是闭凸集。

(2)，。

(3)若f₁、f₂是凸集上的凸函数，且C至少有一个内点，则有。

(4)f在x^*达到整体极小值的充要条件是。

第(4)条可以看作微分学中费尔马(Pierre de Fermat)定理的推广。

需要说明的是，一般凸分析方面的文献中，都允许凸函数在扩充的实数集RU｛±∞｝上取值，为叙述方面起见，我们只考虑在实数集R上取值的情形。

与次微分紧密联系的是共轭函数的概念，这是由芬凯尔1949年引进，又由洛克菲勒70年代前后发展完善的。这一概念是力学和变分学中Legendre变换的推广。设f是Rⁿ上的实值函数．其共轭函数定义为，ξ∈Rⁿ

由定义可知

f(x)+f^*(ξ)≥ξ^Tx，

这叫做Young-Fenchel不等式。

同样，还可以定义f的二次共轭

，x∈Rⁿ

共轭函数总是凸函数。

一般地有f^{* *}≤f，而当f在x次可微时，有f(x)=f^{* *}(x)。

f=f^{* *}当且仅当f是下半连续凸函数。

共轭函数看起来是一个抽象的数学概念，它却有直观的几何意义和明确的经济解释，-f^*(ξ)可以看成是f的上图epi f的支撑超平面(一元函数时称为切线)在纵轴(f轴)上的截距。

设x为产出丛，ξ为产出价格系，f(x)为成本函数，那么利润的最大可能值作为价格的函数由共轭函数f^*(ξ)给出。类似成本和利润这样的对偶关系在微观经济分析中还很多。

次微分与共轭函数之间的关系由下列结果可以看出

当f是下半连续凸函数时，还有更对称的关系式．

虽然共轭函数的定义中不必要求f是凸的，但对凸函数意义较大，它是研究凸规划的对偶性和稳定性的有力工具，这方面洛克菲勒在60年代后期和70年代给出了一系列新颖而深刻的结果，并具有很大的潜力。

1986年，Hiriart-Urruty利用共轭函数给出了极值的一个充要条件：设f是Rⁿ上的可微函数，则x^*∈Rⁿ是f的极小值点的充分必要条件是：(1)▽f(x^*)=0，(2)f^{* *}(x^*)=f(x^*)，在此情况下，f^{* *}在x^*是可微的且▽f^{* *}(x^*)=0．

目前凸函数及凸分析的发展已比较成熟，而其局限性也很明显。

于是近年来，对广义凸函数、非凸函数、非凸分析或非光滑分析的研究方兴未艾，成为热门课题，而凸分析的巨大成功对这一研究一直起着鼓舞和示范作用。此外，近年来对凸集值映射的研究也取得一定进展，但其重要性和实际影响还未被充分认识。

。【参考文献】：

1 Fenchel W. Convex cones, sets and function. Lecture notes, Princeton University, Princeton, N. J. 1951

2 Rockafellar R T. Convex analysis. Princeton University press. Princeton, N. J,1970

3 Avriel M. Nonlinear programming: analysis and methods. Prentice-Hall,Inc,1976

4 Bazaraa M S, Shetty C M. Foundations of optimization, Berlin, Springer (Lecture notes in economics and mathematical systems, 1976,122)

5 Hiriart - Urruty J B. American Mathematical Monthly, 1986,93(7):556～558

6 史树中，凸分析．上海：上海科学技术出版社，1990

7 刘三阳．西安电子科技大学学报，1990，17(1)∶63～69

(西安电子科技大学博士生导师刘三阳撰；游兆永审)