计算力学非线性分析
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第133页(3288字)
计算力学问题,不管它是连续介质力学系统还是有限自由度问题,用数值方法求解时最终归结于在计算机上求解一些基本的数学问题。
从计算角度看,这些基本问题的求解规模,表征了发展的水平,它们可以归结为如下4类问题:
1.Ac=b, x,bεRn,AεRmn为非退化矩阵
2.AX=λX, λεC,XεCm,AεRmxn
3.f(x)=0,f,xRn
4.x=f(xλ),x,fεRn,λεR
这些问题就是:(1)线性代数求解;(2)特征值问题;(3)非线性方程组求解问题;(4)动力系统的全局求解问题。这些问题中n的大小决定了计算力学解题能力与发展水平。
目前的情况是:(1)线性代数方程求解能力,由于采用了稀疏矩阵、消去法等一系列技巧,n可以达到10万阶。(2)特征值问题如果要将全部特征与特征向量求出,一般解题规模n<1000。
(3)如果要将全部实的和复根都求出来,n<100。(4)要将动力系统解的拓扑结构描绘出来,并求出分叉解和各种特殊轨道,目前n=10就已经十分困难了。
这个总的发展水平意味着,对线性问题来说,大部分实际问题可以满足要求,但对非线性2、4来说距离甚远。值得注意的是,上述第2类问题,也可以化归为第3类来求解,即令λ=x0有

为一个二次联立方程组,共有n+1个方程
这就是说上述2.3.4.类问题之所以求解规模仍不能满足需要是因为它实质上是属于非线性的。
对于实际上比较重要的一大类非线性问题,近年来人们开发了不少有效的算法。
其中最重要的是如下两个方法,即延续算法和单形算法。前者发端于计算力学中的荷载增量法;后者发端于数值求解一元非线性方程的二分法。
延续算法 令
f(x,λ)=0 x,f∈Rn,λ∈R (1)
求(x,λ)满足上式。
它的解一般是一维流形,并设去(x0,λ0)是已知的解流形上的一点。解流形是Rn+1中的曲线,不妨记λ=xn+1,则(1)可写为
f(x)=0,f∶Rn+1→Rn (2)
(2)的微分为

令J=(J1,…,Jn+1)其中

式中令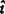 表示在
表示在 中删去第i列。
中删去第i列。
可以证明向量J满足方程(3),将J标准化,引进单位向量

我们来求解(1)的问题化归为微分方程初值问题

利用通常的预报修正办法可求得解x=x(s),参数s称为弧长。所以这一方法又称为伪弧长法。利用它可以成功地渡过结构计算中的极值点。这个方法在数值方法上的发展对应于数学家所称的同伦算法,并成功地应用于求特征值特征向量和求解非线性方程组等问题。
单形算法 考虑非线性方程组
f(x)=0,f∶Rn→Rn (7)
设 ,我们要在Ω内求f(x)=0的根,为此在Ω内引入离散点,并以这些离散点组成Ω的一个单形剖分。这个思想和有限元剖分有某些类似,在单形{x0,x1,x2,…,xn}上它的顶点xi(i=0,…,n)的坐标组成的行列式
,我们要在Ω内求f(x)=0的根,为此在Ω内引入离散点,并以这些离散点组成Ω的一个单形剖分。这个思想和有限元剖分有某些类似,在单形{x0,x1,x2,…,xn}上它的顶点xi(i=0,…,n)的坐标组成的行列式
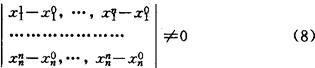
令在单形顶点xi上f(xi)=fi∈Rn(i=0,1,…,n),则当在单形上存在向量w={w0,…,wn}∈Rn+1在0≤ωi≤1(i=0,…,n)内线性方程组

有解时,称这个单形为完全单形。
当f(x)足够光滑,单形充分小,在单形上总存在

满足
f(x*)=0 (11)
一旦找到了一个完全单形,便可以将这个单形加细分为2n个小单形,并逐个检查它的完全性。从而使x*是足够精确地表示。
对于n=1时,便归结于通常的二分法解一元非线性方程。
总结这两个非线性算法,都把求解非线性问题归结为分步线性问题。
由于目前线性问题计算能力已达到相当大的规模,所以这类非线性问题的计算能力也在一定程度上达到满意的结果。延续算法从一点开始,可以把解曲线追踪到充分远。而单形法,可以将一个解逼近到充分精确。当然延续算法如果碰到解曲线的分叉点,则还存在实际的困难需要克服。
考虑动力系统
 ,f∶Rn×R→Rn (12)
,f∶Rn×R→Rn (12)
并令(x0,λ0)为平衡曲线上的某一点,它满足
f(x,λ)=0 (13)
满足(13)的全部解称为静平衡曲线。曲线上的分叉点定义为(x,λ)满足
Reμ=o(14)
这里μ为( )的特征值。
)的特征值。
如果在分叉点Imμ=0,这时具有零特征值,这种分叉对应于静分叉,物理上反映平衡曲线两个以上解分支的交点;否则称为Hopf分叉,物理上反映出现极限环的运动。
目前,利用延续算法和单形法,可以成功地确定高维动力系统静分叉点以及分叉后各解分支的追踪问题。
对于Hopf分叉点的确定,以及分叉后极限环的追踪、则还存在实质上的困难。主要困难在于分叉点判别(14)依赖于求出全部特征值,而目前特征值的求解阶数还不够高,分叉后极限环追踪问题由于自由度迅速增高,变得十分复杂。事实上,Hopf分叉产生的极限环在初始时是一高维空间中的二自由度椭圆,之后随着λ变化它变为高维空间的闭曲线。由于描述它需要将空间成倍地扩展,复杂性也迅速提高。
因此,这个问题的研究大部分还限于三维或四维空间中讨论。
今后计算力学将具有如下的特点:(1)线性问题。在计算机上扩大计算规模将主要地并不是依赖于计算技巧,更主要依赖于硬件发展。这方面两个重要的技术突破预计使线性问题的求解能力将提高两个数量级。第一,国外报导,10000M内存的芯片研制成功;第二,并行计算机出现并发展。(2)自80年代发展的延续算法,静分叉问题的数值方法得到通用软件实现并商品化。
随着力学非线性知识的普及,在工程中求解复杂结构的屈曲、后屈曲行为以及多次屈曲将变为工程设计的常规课题。金属压力加工、注模、流体稳定性等一批实际和理论课题将随之而解决。
(3)Hopf分叉及分叉后极限环追踪问题,对高维空间将得到实际的解决。
(4)计算力学理论上进一步综合。
适应于现代化科学综合性趋势的发展,作为计算力学、计算流体力学与计算固体力学以及一般力学之间的分界将逐渐模糊起来。它们将在统一的计算力学框架之下得到发展。
它们的主要概念与方法将逐步统一。
计算力学不断吸收数学、计算机科学与其他学科的研究成果特别是动力系统、拓扑学、代数几何、计算数学等方面研究成果,改进计算方法。
同时将计算力学的研究成果向物理、天气预报、结构工程等方面推广和转移。
。【参考文献】:
1 武际可.计算结构力学及其应用,1993,2:193~197
(北京大学武际可撰)