分形地貌学
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第704页(4488字)
是一门用现代非线性科学中的分形方法及原理研究地球表面起伏形态及其发生、发展和分布规律的新兴科学。
分形地貌又称为“曼德尔布罗特景观(Mandelbrot landscape)”。“景观”作为一个地理科学术语,由于不同学派或学者在认识和理解角度上的差异,后来出现了同词多义的现象。数学家所用的曼德尔布罗特景观是狭义的景观,主要指地貌,这说明大自然的地貌现象是分形理论最好的研究对象。
分形是一个新的科学名词,指具有标度不变性的集合或体系、现象。
地理学家们长期以来凭直觉已认识到标度不变性在地貌中的客观存在。例如,在野外拍摄的地貌照片中通常附上已知尺寸的某件普通物品(如地质锤、人体等),否则就无法断定原形体的大小,这就是标度不变性的一种反映。分形理论是由法国曼德尔布罗特(B.B.Mandelbrot)创立的。分形的外在表现是极其破碎或非常无规或十分复杂,具有无穷的细节,在不同标度(放大率)下呈现同等程度的复杂性。而其内在本质是有自仿射性(或自相似性)。
以直线为基础的传统的欧几里德几何无力描述大自然的真实面貌,而让位于以描述客观自然(如处处连续处处不可微的曲线)为己任的分形理论,分形地貌学即随之而诞生。分形有简单分形和多分形(multifractals)两类,后者指的是不均衡的须用多个标度指数来刻画的复杂分形。定量描述分形外貌特征、构造演化规律的参数叫分维(fractal dimension),有多种形式和计算方法。
分形地貌学的主要任务是以分维为工具来刻画地表形态,并以分维为中介参数建立地貌与内部机制之间的联系。
在现阶段,分形地貌学作为理论地貌学的一个新分支,已在两方面展开工作。
一是凭借地学家和数学家的丰富想象,用计算机创造出各种标准的理想“地貌”,在通过研究这些地貌,找到塑造某些特殊地貌的内在动力学机制。
目前至少已有这样的共识:地貌尽管千姿百态,但产生的机制可能很简单,即内外力相互作用的结果。
在理论上,可用维尔斯特拉斯-曼德尔布罗特(Weierstrass-Mandelbrot)随机函数、分式布朗运动(FBM)和复函数迭代法来产生,这是曼德尔布罗特景观的主要来源,已达以假乱真的程度。如海岸线,就可用科赫(von Koch)曲线来构造。
这种地貌的分维可能严格准确地计算。另一方面,分形地貌学必须直面现实,对大自然中客观存在的各类地貌进行卓有成效的研究,求出有关分维,作出区域划分,进行理论地貌学阐述。
计算分维的方法一般是R/S分析,谱密度分析或时间序列分析(如GP算法)。
分形地貌学目前已建立如下基本原理。
(1)仿射变换原理。地貌是一类满足自仿射变换的分形曲面,内外力的作用是发生变换的根本原因。
(2)开放性原理。地貌是地理系统长期演化和局部耗散失稳的结果,在此过程中地貌系统与外界进行的物质、能量、信息交换具有分形输运的性质。
(3)层次性原理。地貌系统中的各个要素的地位和作用不同,系统和要素是相对的。
一个系统可称为上个系统的要素,同样,一个要素对下个系统来说又可称为系统。(4)分解协调原理。
在认识和研究地貌时,可将其活动过程或组成结构分解为若干相互衔接和关联的部分,通过协调关系或调整结构,可使系统的功能达到预定的效果。其数学形式为多分形(multifractals),其意义是奠定了区域开发、利用的理论基础。
(5)稳定性原理。地貌在外界作用下保持和恢复其原有状态及内部结构功能的性质。一种地貌要存在,必须有相对稳定性,即它的状态参量在短时间内是不随时间变化的。(6)突变性原理。
在一定时空区域内的地貌系统,由于内部非线性机制作用,会自发地向临界状态进化。处于临界状态的地貌系统,在空间上具有分形结构,在时间上具有负幂律(f-β)行为。
若有某一微扰触动就会发生从一种稳态向另一种稳态的跃迁。(7)级差原理。若地貌是分形集M,M是由分属于不同层次的子集Gk(k=0,1,2……,k称为初次)构成,GK可以某种方式(结构、组成或运动性)与M相似,则K越小,结构越简单;K越大,结构越复杂。级次k越接近的子集越相似,反之,k相差越大则越不相似。
(8)分维相关性原理。地貌系统中各局域分维之间,局域分维与整体分维之间具有相关性,满足一定的运算规则。
这一原理共包括7条定理:定理1(积和原理):若集合S是两个分维为D1和D2的分形子集S1和S2的乘积,则S的分维D=(D1+D2);定理2(和并原理):若集合S是两个分维为D1和D2的分形子集S1和S2的和,且D1>D2,则S的分维D介于D1和D2之间,最大值为D1;定理3(匹配原理):若分形子集S2和S1要有效地组成分形集S,则要求S2和S1的分维(或局域分维)相等或接近;定理4(包容原理):若分形集M欲包含子集S,则要求S的分维不大于M的分维;定理5(相交原理):在d维欧氏空间中,两个分维分别为DA和DB的分形子集的交集的维数D=(DA+DB-d);定理6(赫斯特原理):若曼德尔布罗特景观的赫斯特(Hurst)指数为H,则在d维欧氏空间中的分维 ,其中β是谱指数1<β<3,而0<H<1;定理7(相关原理):若分式布朗运动(fBM)地貌的赫斯特指数为H,相关函数为C(t),则C(t)=22H-1-1。当
,其中β是谱指数1<β<3,而0<H<1;定理7(相关原理):若分式布朗运动(fBM)地貌的赫斯特指数为H,相关函数为C(t),则C(t)=22H-1-1。当 时呈正相关;
时呈正相关;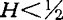 时呈负相关;
时呈负相关; 时即随机运动(不相关)。
时即随机运动(不相关)。
由此可进行预报。
分形地貌学的诞生和发展有一个历史过程。
1961年理查逊(L.F.Richardson)发现海岸线的长度L依赖于测量的尺度r,L(r)=Kr1-D(K为常数),即随着尺度的缩小,长度增长。1967年,曼德尔布罗特发表了《英国海岸线有多长?》的划时代论文,他把D解释成分维,从而标志着分形地貌学的诞生。
1975年,曼德尔布罗特称为“宣言加手册”的专着《分形:形态,机遇和维数》法文版正式出版,1982年英文版《大自然的分形几何学》与读者见面。
此书有近 的篇幅是讨论曼德尔布罗特景观的,并附有许多精美的插图。
的篇幅是讨论曼德尔布罗特景观的,并附有许多精美的插图。
在水系方面,1945年河顿(R.E.Horton)提出的水系结构定律,实际就是一个分形模型。1988年以来,罗索(R.Rosso)、巴伯拉(L.Barbera)和耶尔姆费特(A.T.Hjelmfelt)等人在这方面进行了许多研究,如发现分维Df=2lnRL/lnRb,或分维统计值 ,其中RB、RL分别为分枝比和长度比。
,其中RB、RL分别为分枝比和长度比。
1987年12月,美国地理物理联合会在旧金山举行的秋季学术会议上召开了“地球物理学中的分形”专题讨论会,内容涉及地貌、地表水系、地下渗流和海岸等领域的分形问题。斯诺(R.S.Snow)对西俄亥俄河流域的12条形态各异的河道进行了详细研究,他认为把流径作为分形曲线来描述是恰如其分的。马林维诺(A.Malinverno)和马雷斯切尔(J.C.Mareschal)讨论了海底地形的分形性质,吉尔伯特(L.E.Gilbert)则研究了大陆地形。福克斯(G.Fox)和吉尔伯特两人指出了在对地形剖面这样的自仿射分形进行直接分析时所遇到的困难。1991年,李后强、艾南山在渗流(Percolation)模型基础上,发现流域的侵蚀积分值P与河网密度ds有关系P=EdsD,其中E是侵蚀模数,D为分维。并且,P可从斯特拉勒(Strahler)曲线上直接求出,P=1-。
xdy。其中,X=a/A,y=h/H,a是流域等高线图上量出的每一条等高线以上的面积,h是每条等高线与流域最低点的高差,H为流域最高点与最低点的高差,A为流域面积,x、y均在[0、1]内取值。
得到侵蚀早期分维D=0~0.75,中期D=0.75~1.89,晚期D=1.89~2.0。
奥地利沙伊德格尔(A.E.Scheidegger)1991年出版的《理论地貌学》第3版,已专门介绍了分形的应用。1992年李后强、艾南山等用稳定分布研究了风沙流的结构,发现了风沙流分布的负幂律M(h>h0)=ch-D(M为沙子含量,h为高程,D为分维,c为常数)和运动的标度律, (v为地表耗散系数,β为空气弥散系数,A为常数,D为分维,h为高程,ξ为风速),特别是用湍流的多分形特征研究了风沙地貌的形成机制。
(v为地表耗散系数,β为空气弥散系数,A为常数,D为分维,h为高程,ξ为风速),特别是用湍流的多分形特征研究了风沙地貌的形成机制。
分形地貌学的问世虽有30余年的历史,但真正作为一门科学受到重视仅是近年的事。
预计今后的趋势是:大范围(甚至全球性)地观测地貌分维,并将其规范为一种应用性参数,将是地貌学家的一项重要工作。使用的数学工具将是非线性时间序列、功率谱分析和子波变换。其中,根据自组织临界状态研究地貌突变机制,会激发一些学者的兴趣,并可能有实质性突破。
利用间歇湍流的多分形理论成果讨论流域地貌的发育和风沙地貌的机制(或土地沙化)是一个富有活力的研究领域。把多分形同信息熵联系,深化地貌熵的内涵和拓展信息熵的应用,也是大有可为的。把从时间序列观测的分维作为独立变量的个数,进行非线性动力学反演,求出地貌演化的动力学方程,将是引人入胜的新方向,并有可能是理论地貌学家今后几十年的奋斗目标。
。【参考文献】:1 Mandelbrot B B. The Fractal Geomery of Nature W H Freeman, 1982
2 Pcitgcn H O, Saupc D. The science of Fractal Images, Springer-Verlag, 1988
3 Fcdcr J Fractals. Plenum Press, 1988
4 Scholz C H, et al. Fractals in Geophysics, Pure and Applied Geophysics, 1989,131:1~2
5 李后强,等.分形与分维.四川教育出版社,1990
6 Li H Q,Chen S H,et al.Chinese Science Bulletin,1991,36(15)∶1319
7 Schcidegger A E.Theoretical Geomorphyology,Third completely Revised Edition,Springer-Verlag,1991
8 李后强,等.自然杂志,1991,4∶245
(四川大学物理系李后强教授撰;艾南山教授审)