Morita对偶

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第23页（3808字）

环论中的Morita对偶理论，是除环上向量空间对偶的推广，由Morita和Azumaya在20世纪50年代末建立的。

1974年，Anderson和Fuller介绍了Morita对偶理论。1992年，薛卫民曾对该理论进行了较详细地论述。

设V为域F上向量空间，记V^*=HomF(V，F)。若维(V)＜∞，则维(V)=维(V^*)=维(V^{* *})，从而。

若维(V)=d=∞，则维(V^*)=｜F｜^d＞d，从而，同样V。

设D^V(V_D)为除环D上的左(右)向量空间，V^*=HomD(V，D)为D上右(左)向量空间，若维(V)＜∞，则。

因此，HomD(－，D)导出了有限维左D－向量空间与有限维右D－向量空间之间的一个对偶。

令R和S为含单位元的结合环，称左R－模范畴R－Mod和右S－模范畴Mod－S之间存在一个Morita对偶，如果存在完全子范畴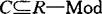和完全子范畴，这里C和D关于子模和商模封闭且包含所有的有限生成模，使有反变加法函子F：C→D及G：D→C满足及。

此时，称环R具有(左)Morita对偶，环S具有右Morita对偶，该对偶可由(F，G)导出。

Morita(1958)和Azumaya(1959)证明(F，G)导出一个Morita对偶当且仅当存在忠实平衡双模_RE_S使得_RE和E_S都是内射上生成元(cogenerators)，且有和Homs(－，E)，此时C和D就是由所有的_RE_S－自反模组成。

因而，也称双模_RE_S导出Morita对偶。若有R－双模_RE_R导出Morita对偶，称之为Morita自对偶。

因此，要证明一个环R具有Morita自对偶，首先要证明R具有Morita对偶，该对偶由某个双模_RE_S导出，然后证明。Morita和Azumaya证明了每一个交换Artin环均具有Morita自对偶，他们还证明了一个左Artin环R具有Morita对偶当且仅当每一个不可分解的内射左R－模是有限生成的。利用Cohn(1966)和Schofield(1985)的除环构造，可给出一个Artin环R使得R不具有Morita对偶，或R具有Morita对偶但不具有Morita自对偶。

设双模_RE_S导出Morita对偶，若R为左或右完全环，则R必为左Artin环，此时S为右Artin环，且模M为_RE_S－自反模，当且仅当M是有限生成的，即Artin环的Morita对偶基本上保持了除环上向量空间的对偶性质。

若R为(双边)Artin环，则S是否为左Artin环还是一个未解决的问题。若R为左Noeth环，不能推出S为右Noeth环，反例见参考文献［9］的第5章，但若R为(双边)Noeth环，可推出S为右Noeth环，此时S是否为左Noeth环还是一个未解决的问题。

若R－双模_RR_R导出Morita对偶，称环R为PF－环或上生成元环，此时_RR和R_R都是(内射)上生成元，PF－环R称为QF－环，若R满足以下4个等价条件之一：(1)R为左Artin环。(2)R为右Artin环。(3)R为左Noeth环。

(4)R为右Noeth环。

关于一般环的Morita对偶理论，线性紧性起着重要的作用。

设M为一个模。

设m_i∈M，M_i≤M，i∈I，称族(m_i，M_i)_i∈I为可解的，如果存在m∈M使得m－m_i∈M_i，，称族(m_i，M_i)_i∈I为有限可解，如果对任意有限子集，族(m_i，M_i)_i∈I。都是可解的。称模M为线性紧模，如果M的任何有限可解的族都是可解的，线性紧模是Artin模的一个推广，环R称为左(右)线性紧环，如果左(右)模_RR(R_R)是线性紧模。

1970年Muller证明了环R具有Morita对偶当且仅当R为左线性紧环且R－Mod的极小内射生成元_RE为线性紧模，此时_RE_S导出Morita对偶，这里S=End(_RE)。

若_RE_S导出Morita对偶，则左R－模(或右S－模)M为线性紧模，当且仅当M是_RE_S－自反模。若R为具有Morita对偶的可换环，则R具有Morita自对偶。Müller问：是否每一个交换线性紧环具有Morita对偶?1990年，Anh给予了肯定回答。

设R为左线性紧环(则R为半完全环)，设_RE为有限上生成的内射上生成元。若_RE还是线性紧模，则_RE_S导出Morita对偶，这里S=End(_RE)为右线性紧环，E_s为线性紧的有限上生成的内射上生成元。

这是Müller定理的一个推广。若R^ES导出Morita对偶且R为(双边)线性紧环，则S是否为左线性紧环还是一个公开问题。

若D是一个除环，则幂级数环D［［x］］具有Morita自对偶，该对偶可由D［［x］^］－双模导出。

若R为一般的具有Morita对偶的环，则是否幂级数环R［［x］］不一定具有Morita对偶。尚且不知。

对于任意环R，多项式环R［x］均不是左线性紧环，因此R［x］不具有Morita对偶。

设有环扩张R≤S，人们探讨在什么条件下由R(或S)具有Morita对偶或自对偶可推出扩环S(或子环R)也具有Morita对偶或自对偶。

1989年，薛卫民指出，对于环的有限扩张R≤S(即_RS和S_R为有限生成模)，环R和环S的Morita对偶性没有联系。1984年，Lemonnier证明若R≤S为有限三角扩张，则R具有Morita对偶可推出S也具有Morita对偶。虽然逆命题还未解决，逆命题对左Artin环S成立。1990年，Kraemer证明除环上的有限正规扩张环均具有Morivta自对偶。

1983年，Azumaya称一类Artin环为正合环，证明它们具有Morita对偶且预言它们具有Morita自对偶。

这一预言还未解决，甚至两类特殊的正合环，局部分配环和Artin双环，它们是否具有Morita自对偶还未得到证实。一类特殊的局部分配环一序列环，它们具有Mortita自对偶。这一结果由Waschbusch(1986)及Dischinger和W．Müller(1984)得到证明。

综上所述，Mortita对偶理论的研究多年来一直在进行，取得了一定的进展，但还有许多问题未解决，需要进一步研究与探讨，使之更加系统化，内容更加丰富，成为环论研究的一个重要组成部分。

。

【参考文献】：

1 Morita K. Duality for modules and its applications to the theory of rings with minimum condition. Tokyo Kyoiku Daigaku ,Ser A6,1958,83～142

2 Azumaya G. Amer J Math,1959,81;249～278

3 Miiller B J. J Algebra,1970,16:60～66

4 Anderson F W &Fuller K R. Rings and Categories of Modules,Springer-Verlag. Berlin, 1974(second edition,1992) Azumaya G. J Algebra, 1983,85:477～489

5 Lemonnier B. Dimension de Krull et dualite de Morita dans les extensions triangulaires, Comm. Algebra, 1984, 12: 3071～3110

6 Anh P N. Morita duality for commutative rings, Comm Algebra, 1990,18:1781～1788

7 Kraemer J. Math J Okayama Univ,1990,32:103～109 Weimin Xue. Lecture Notes in Mathematics 1523, Springer-Verlag ,Berlin, 1992

(福建师范大学薛卫民教授撰；许永华审)