大系统的稳定性

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第36页（3129字）

这种理论是从20世纪60年代开始发展起来的。

早在1959年，秦元勲首先提出了稳定性理论中方程组的分解问题。随着科学技术的迅速发展，系统规模的扩大、计算机的广泛应用，控制系统也出现了多层次的复杂化与大型化，促使人们不得不研究大系统理论。

考虑系统

i=1，…，l．这里Z_i∈Rⁿ_i，t∈J=［t₀，+∞)，f_i：Rⁿ_i×j→Rⁿ_i，g_i：Rⁿ₁×…×Rⁿ_l×J→Rⁿ_i．在下面总假设，对于所有的t∈J，f_i(Z_i，t)=0的充要条件是Z_i=0，令，x^T=(Z₁^T，…，)∈Rⁿ。

及

故有

g(x，t)^T=［g₁(x，t)^T，…，gl(x，t)^T］

我们将系统(1)写成

(2)

显然，f：Rⁿ×J→Rⁿ，g：Rⁿ×J→Rⁿ以及h：Rⁿ×J→Rⁿ。

我们总假设，对于所有t∈J，h(x，t)=0的充要条件是x=0。

由方程(2)所描述的系统可以认为是由下面l个系统

(ψ_i) Z_i=f_i(Z_i，t)(i=1，…，l) (3)

的一个非线性和时变的关联。

系统(2)称为复合系统(ψ)，或称为关联系统(ψ)，或称为具有分解(∑_i)(由方程(1)描述)的大系统(ψ)、方程(3)被称为第i个孤立子系统(ψ_i)。

通常处理大系统问题可分为如下3个步骤：①将大系统(ψ)(方程(2))，分解成1个孤立子系统(ψ_i)(方程(3))，具有分解(∑_i)(方程(1)。

②对于每个孤立子系统(ψ_i)应用Λяnyнoв第二方法(重要的是具体地构造出Λяnyнoв函数)。

③整个系统的定性分析，由子系统及关联结构的定性性质决定。

研究大系统零解的稳定性，通常采用以下两种方法：①向量Aяnyнoв函数方法：以子系统的Λяnyнoв函数V_i作为V的分量，用比较原理，由已知系统(或低阶系统)的稳定性来得出大系统的稳定性。②标量Aanyнoв函数方法：取子系统的Λяnyнoв函数的加权和作为大系统的Λяnyнов函数，即取，再利用Λяnyнов定理，以得出大系统的稳定性。

值得注意的是由章毅和张毅所提出的处理大系统稳定性的参数变易法，近年来已得到广泛的应用。

大型动力系统可视为互相作用分量(子系统)的一个不均匀结构，分量(子系统)之间的互相作用在强度和形状上悬殊很大。一组子系统能暂时地与其余子系统分离，导致了大型动力系统结构上的变化，因此我们需要考虑系统在结构变化(结构扰动)下的稳定性，即关联稳定性。借助于有向图和互联矩阵等概念。

利用上面所提到的研究大系统的向量Λяnyнoв函数方法与标量Λяnyнoв函数方法，可以研究大型动力系统的结构稳定性。

为了说明标量Λяnyнов函数方法的实质。

我们证明下面定理。首先作下面约定，我们称孤立子系统(ψi)具有性质A，如果存在一个连续可微函数V_i：Rⁿ_i×J→R，及函数ψ_i1，ψ_i2∈kR，ψ_i∈K及常数6_i∈R，使得不等式

对于所有的Z_i∈Rⁿ_i及所有t∈J成立。

定理，具有分解(∑_i)的复合系统(ψ)的零解是大范围(全局)一致渐近稳定的，如果下面的条件满足：①每个孤立了系统(ψ_i)具有性质A；②给定V_i及假设①中的ψ_i3，存在常数a_ij∈R，使得不等式j对所有Zi∈Rⁿ_i(i=1，…，l)及t∈T成立；③给定了假设①中的б_i，存在一个1－向量α^T=(α₁，…，α_l)＞0，使得矩阵S=(S_ij)为负定，其中

证：对复合系统(ψ)，我们选取如下的Λяnyнoв函数：

这里函数V_i(Z_i，t)由假设①中给出，α_i＞0(i=1，…，l)是由假设③中给出的常数，显然V(x，t)连续可微，且对于所有的t∈J，有V(0，t)=0。由于每个弧立子系统(ψ_i)具有性质A，得出

由假设ψ_i1，ψ_i2∈KR得出：V(x，t)是正定的，具有无限小上界，且有无限大性质，事实上，存在ψ₁，ψ₂∈KR，使得

ψ₁(｜x｜)≤V(x，t)≤ψ₂(｜x｜)

对所有x∈Rⁿ及t∈J成立，因

由假设①及②得出

令

R=(r_ij)是l×l矩阵，其中

已知

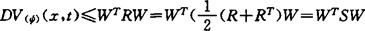
这里S=［S_ij］是假设③中所给出的矩阵，因为S是对称的，故其所有特征值为实的，由假设③S是负定的，故其特征值均为负，所以λ_M(S)＜0，又有

因此DV_(ψ)(x，t)是负定的(对所有x∈Rⁿ及t∈J)故对所有x∈Rⁿ及t∈J，有

DV_(ψ)(x，t)≤λ_M(S)ψ₃(｜x｜)

其中λ_M(S)＜0，因此复合系统(ψ)的零解是大范围一致渐近稳定的。

以上处理常微分方程大系统稳定性的方法，已用于研究离散大系统的稳定性，离散动力系统在结构扰动下的稳定性，Volterra积分微分方程大系统的稳定性，具有无穷时滞中立型积分微分方程大系统的指数稳定性等等，并在控制理论中得到广泛的应用。

。

【参考文献】：

1 王慕秋．科学记录，1960，4(1)

2 Michel A N, Miller R K. Qualitative Analysis of Large Scale Dynamical Systems. New York: Academic Press, 1977

3 Siljak D D. Large-Scale Dynamical Systems:Stability and structure. Elsevier North-Holland, Inc New York,1978

4 王联，王慕秋．非线性常微分方程定性分析，哈尔滨工业大学出版社，1987

5 章毅，王慕秋．科学通报，1990，35(2)

6 Wang Muqiu，Wang Liian，Du Xuetang．Acta Math Appl，1992；8(1)

(中国科学院数学研究所王慕秋研究员撰)