黎曼流形的谱
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第87页(4685字)
又称谱几何,是大范围分析领域中整体微分几何的一个重要分支。
集泛函、拓扑、复变,偏微分方程、代数等内容于一体,从而有力地推动了几何学科的发展。谱几何中所采用的几何方法广泛地应用在其他数学与物理学科之中,已成为现代基础数学理论研究的一个热点。
设q是[a,b]上连续函数,则[a,b]上一维的具有Dirichlet边界的Schrodinger方程

的Sturm-Liouville特征值问题,是指找的那些λ值称为特征值,使得Schrödinger方程具有非零的C2类函数y的解。
R.Courant于1953年引进的Cauchy问题:

的解uλ。
设[a,b]上函数uλ(x)零点的个数记作N(λ),即N(λ)=#{uλ(x)在[a,b]中x的零点},利用Sturm比较定理,可以证明N(λ)是一个递增的、右连续函数,当λ→∞时,N(λ)→+∞,并且那些不连续点正好是Schrödinger方程的解。
J.Dieudonné于1975年将Schrodinger方程化为积分方程,利用紧致算子谱理论证明存在特征值的无穷序列0<λ1<λ2……∞.
如果D是R↑(n中具有逐段光滑边界B的有界区域,考虑特征值问题:

这里 ,
,
H.Weyl于1946年和M.Kac于1966年,把D想像作鼓面,把特值值0<r1<r2<r3<……取作基调,倾听鼓声,以得到鼓面的形状,由 可判定鼓的面积和周长等等,根据这些物理背景和几何模型引入4种类型黎曼流形谱的概念。
可判定鼓的面积和周长等等,根据这些物理背景和几何模型引入4种类型黎曼流形谱的概念。
(1)闭的谱问题。设M是紧致的、连通的黎曼流形,△是M上C2或C∞函数的Laplace算子,则黎曼流形(M,g)的谱是λ的全体:λ∈R,使得△f=λf存在非平凡解 (或f∈C2(M)),黎曼流形(M,g)的谱记作Spec(M,g),称λ为特征值(或谱值)。
(或f∈C2(M)),黎曼流形(M,g)的谱记作Spec(M,g),称λ为特征值(或谱值)。
(2)Neumann谱问题。
设黎曼流形(M,g)的 ,M紧致且连通,Spec(M,g)是λ的全体:λ∈R,使得△f=λf存在非平凡解
,M紧致且连通,Spec(M,g)是λ的全体:λ∈R,使得△f=λf存在非平凡解 。
。
并满足边界条件 ,其中v是
,其中v是 上向外的单位法向量场。
上向外的单位法向量场。
(3)Dirichlet谱问题。
设黎曼流形(M,g)的 ,M紧致且连通,Spec(M,g)是λ的全体:λ∈R,使得存在△f=λf的非平凡解
,M紧致且连通,Spec(M,g)是λ的全体:λ∈R,使得存在△f=λf的非平凡解 。并满足边界条件
。并满足边界条件 。
。
(4)混合型谱问题。
设黎曼流形(M,g)的 紧致且连通,N是
紧致且连通,N是 的开子流形,Spec(M,g)是λ的全体:
的开子流形,Spec(M,g)是λ的全体: ,使得△f=λf存在非平凡解
,使得△f=λf存在非平凡解 ,并满足边界条件:在
,并满足边界条件:在 上,f=0;在N上,vf=0。
上,f=0;在N上,vf=0。
对于上述四类谱问题,Spec(M,g)构成一个序列{0=λ0<λ1<λ2<……∞),是离散的,且趋向于+∞}。对于每一个特征值λ,△f=λf的解空间记作P↓(λ(M,g),称为与λ相关的特征子空间,Pλ(M,g)的元素称为特征函数,每一个Pλ(M,g)是有限维的,其维数称为特征值的重数。
M.Berger1971年出版专着《Le Spectre d′une variété Riemannienne》——黎曼流形的谱,把谱的研究推向纵深发展。M.Berger和P.Bérard于1982年列出谱几何研究的详细文献资料,既总结了前阶段这一领域的科研成果,又指明了今后的研究课题。S.Gallot,于1986年在法国数学会杂志《Astérisque》上,系统地总结了谱几何的研究成果。特别是P.Bérard于1986年由Springer LN1207出版《Spectral Geometry:Direct and Inverse Problems》——谱几何的正问题和反问题,将谱几何的研究推向高潮。
目前,谱几何的研究热点是:
(1)谱几何的正问题。计算流形的谱,例如球面,实射影空间,复射影空间,平坦环面等流形谱的计算早已解决,但至今尚有许多流形谱的计算却十分困难,例如,球面三角形区域等等。
(2)特征值的估计。在许多着作与文献中,都对第一个非零特征值λ1进行估算,确定其上限与下控。
结合黎曼流形的几何特征,进一步估计λ1或λ2,并研究Pinching问题。
(3)利用谱的结果,得到流形的一些几何性质。若Spec(M,g)=Spec(N,h),能否断定(M,g)或(N,h)是等距的、同胚的或者微分同胚的,这是一个十分有趣的研究课题。
(4)因为作用在f∈C∞(M)上的Laplace算子是一个实的、正定的、自伴随的、二阶椭圆型微分算子,它与偏微分方程学科的研究密切相关。为此,可以研究一类更为广泛的二阶线性椭圆型方程:△U-vU=λU,式中△表示流形M的Laplace算子,v∈C∞(M),称为位势,称常数λ为Schrōdinger算子Δ-v的特征值,对应的解称为特征函数,关于Δ-v的特征值的讨论已引起大家的关注。
(5)设(M,g)是闭的黎曼流形,Ap(M)表示M上p次外微分形式(p≤dimM)所生成的空间,作用在Ap上的微分算子△=δd+δd,式中d是外微分算子,d:Ap-1→Ap;δ是余微分算子.δ:Ap→Ap-1。当f∈A°(M),δf=0。当α∈Ap(M),1≤p≤n,δα=(-1)n(p+1)+1*d*α,这里*是Hodge星算子,即若α∈Ap(M),则*α∈An-p(M)。由此可见,△=dδ+δα是Ap(M)→Ap(M)的线性映射,称为黎曼流形(M,g)上的Laplace-Beltrami算子,或简称Laplace算子。满足△α=0的微分形式α称为调和形式。
特别地,满足△f=0的函数f∈A°(M)称为调和函数。调和形式的应用以及满足△α=γα,α∈Ap(M)的p次微分形式谱pSpec(M,g),(当p=0时,°Spec(M,g)即为Spec(M,g)),它的研究尚待进一步深入。
(6)谱几何主要用于讨论热方程和波动方程基本解(简写作SFEC),所谓基本解是指 上的一个函数E.它满足下述3条公理:
上的一个函数E.它满足下述3条公理:
SFEC1 E在 上是连续函数,对第2个变量是C2的,对第3个变量是C1的。
上是连续函数,对第2个变量是C2的,对第3个变量是C1的。
SFEC2 L2E=0。此处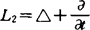 ,而△2是指对第2个变量的拉普拉斯算子。
,而△2是指对第2个变量的拉普拉斯算子。
SFEC3 对任何m∈M,有

这里的δm是在m点的Dirac测度。
于是,当t→0+时,SFEC的渐近展式为

其中 的一个法正交基,则
的一个法正交基,则

黎曼流形(M,g)上波动方程的基本解(或波动核)是函数E(t,x,y),其中(t,x,y)∈R×M×M,它满足

在谱几何意义下,它是算子 的核。
的核。
例如,(S2,g0)的波动核是
其中C2为某一常数,而函数

波动方程的方法是由L.Hormander于1960年以后研究函数N(λ)而引入的,它可用黎曼流形的谱和流形上闭测地线长度之间的一些关系式而加以说明,1973年Y.Colin DE Verdiere以及1975年J.J.Dvistermaat解决了这个问题。
这类偏微分方程的研究同物理上布朗运动与概率论的研究有联系,通过参考文献2可以进一步予以探讨。
。【参考文献】:1 Minakshisundaram S, Pleijel A. some properties of the Laplace operator on Riemannian manifolds,Canad. J Math, 1949
2 Lichnerowicz A. geometric des groupes de transformation, Dunnod, Paris, 1958
3 Kac M. Can one hear the shape of a drum.Amer. Math. Monthly, 1966,73
4 Mckean H P,Singer I M. Curvature and the eigenvalues of the Laplacian,J Diff Geom, 1967,1
5 Cheeger J. The relation between the Laplacian and the Diameter , Archiv Der Math ,1968,19
6 Saki T. on Riemannian manifolds,Canad J,Matn. 1949,1
7 Berger M.Gauduchon P,Mazet E. Le spectre d'une variete riemannienne,Lecture Notes in Math,n° 194,Springer 1971
8 Berard P, Berger M. Le spectre d'une variete riemannienne en 1982,Kaigei Publications,1983
9 Berard P. Spectral geometry: direct and inverse problems, 1MPA. 1986
10 马传渔.黎曼流形的谱.南京:南京大学出版社,1993
(南京大学马传渔教授撰;莫绍揆审)