黎曼流形与洛仑兹流形中的常平均曲率子流形
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第89页(4231字)
研究具有常平均曲率的完备黎曼流形到空间形式中的等距浸入涉及到流形上的分析,主要研究方法是利用E.Cartan引进的活动标架法。
对极小曲面,1915年Bernstein证明了:
定理1 三维欧氏空间中定义在全平面上的完备极小曲面是平面。
由此产生了Bernstein问题。在n-1维欧氏空间Rn-1全体上定义的n维欧氏空间Rn中的完备极小超曲面是超平面吗?针对这一问题,E.de Giorgi(1965)、F.J.Almgren(1966)和J.Simons(1968)分别对n=4,5和n≤8肯定地解决了Bernstein问题。对于n≥9,E.Bombieri,E.de Giorgi和E.Giusti于1969年给出了Bernstein问题的否定回答。
对Bernstein问题的球面解释,1936年为Myers证明。
定理2 如果一个n维闭黎曼流形被极小地浸入在单位球面Sn+1(1)中的闭半球面中,则M是超球面Sn(1)。
Myers定理现已被成庆明推广到完备的黎曼流形。Myers定理的证明方法是证明从M上的任意点到闭半球面的边界的距离函数是上调和函数,再由Hopf的极大值原理得知这个距离函数恒等于零。
因此M是全测地的,即为超球面Sn(1)。
1968年Sirnons利用此思想方法研究球面中的极小子流形,为极小子流形的研究做出了重要贡献。
他获得了由第2基本形式模长的平方满足的一个二阶线性椭圆型偏微分方程,并利用它证明下述定理。
定理3 设M是单位球面Sn+p(1)中的n维闭极小子流形,则
∫M…[2-1/p)S-n]Sdv≥0,其中S为M的第2基本形式模长的平方。
Simons的文章问世之后,引起了几何学家的广范兴趣,先后发表百篇研究空间形式中极小子流形的文章。根据Simons定理我们知道,如果S≤n/(2-1/p),则S=0(这时M是全测地的)或者S=n/(2-1/p)。Lawson(对p=1),Chern(陈省身)doCarmo和Kobayashi(对任意的p)分别独立地确定了S=n/(2-1/p)的闭极小流形。他们获得:
定理4 S4(1)中的Veronese曲面和Sn+1(1)中的Clifford torus是Sn+p(1)中唯一满足S=n/(2-1/p)的闭极小超曲面。
上述结果也已经被推广到完备的情形。1974~1975年邱成桐连续发表了两篇关于常平均曲率子流形的文章。
他从几个不同的角度研究了这类子流形,并提出了一些很有意义的问题。对应于Simons的结果Yau证明了利用截面曲率的限制代替对S的限制。
定理5 设M是单位球面Sn+p(1)中的闭极小子流形。
如果M的截面曲率大于等于(p-1)/(2p-1),则M是全测地的,或S4(1)中的Veronese曲面或Sn+1(1)中的Clifford torus。
现在利用截面曲率研究极小子流形的更进一步的结果也已经被做出。综合从1979年至今关于利用Ricci曲率Pinching条件所得结果,我们有
定理6 设M是Sn+p(1)中的闭极小子流形如果其Ricci曲率满足

则M是全测地的,或n=2k且M=Sk(2)×Sk(2)或n=4而且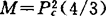 .其中
.其中 是二维复射影空间。
是二维复射影空间。
关于具有常数量曲率的闭极小超曲面,Chern有如下的猜想:对于单位球面Sn+1(1)中具有常数量曲率的闭极小超曲面,S的值是离散的。
Simons证明S的第1、2个值分别是0和n,并且Chern等给出了S=n时M是Clifford torus。关于Chern的猜想,彭家贵,滕楚莲,杨洪苍和成庆明从1982年至今证明了如下结论。
定理7 设M是S4(1)中的3维完备极小超曲面。
如果S≤6且为常数,则S=0,3或6。特别当M是闭极小超曲面时,M是等参的。
定理8 设M是Sn+1(1)中n维闭极小超曲面。如果S≤5n/4且为常数,则S=0或n。
根据已知的闭极小超曲面的例子和定理8,我们可以推测S的第3个值可能是2n。
这也是我们今后要研究的问题之一。
另一方面。在Simons定理的启发下,1971年Nomizu和Smyth研究了黎曼空间形式中的常平均曲率的完备超曲面,他们获得:
定理9 设M是黎曼空间形式Mn+1(c)(c≥0)中的常平均曲率完备超曲面。
如果M的截面曲率非负且数量曲率为常数,则M是全脐的或者M是两个非负常曲率流形的黎曼积。
1974年Yano和Ishihara在法曲率平坦的条件下把Nomizu和Smyth的结果推广到任意余维数的情形。对于常平均曲率子流形类似于Simons的Pinching条件,从1974年至今在不断发展和改进的情况下,可归结为如下定理。
定理10 设M是单位球面Sn+p(1)中的n维具有平行平均曲率向量的紧致子流形,如果S≤C(n,p,H),则M是全脐的,或M为Sn+p(1)中n+1维球面 中的Clifford torus或为
中的Clifford torus或为 中的Veronese曲面,其中H为平均曲率。
中的Veronese曲面,其中H为平均曲率。
当M是完备的情形,部分结果也成立。特别对于n=3的情形我们有
定理11 黎曼空间形式M4(c)(c≥0)中具有非负常数量曲率的非零常平均曲率完备超曲面仅有S3(c1)(c1>c),Rk×S3-k(c1)(k=1,2),S1(c1)×S2(c2)和Veronese曲面的管子(tube)。
常平均曲率子流形的研究要比极小子流形的研究困难的多。但人们自然会问对极小子流形成立的结果,常平均曲率子流形是否成立?因此今后一段时间内,人们会对黎曼空间形式中的常平均曲率完备子流形做更进一步深入的研究。
对于非空间形式中的完备子流形的研究也可能是今后发展方向之一。
作为Bernstein型问题的洛仑兹解释,Calabi(对n≤4)、S.Y.Cheng(郑绍远)和Yau(对任意的n)已经证明
定理12 Minkowski空间 中的完备极大类空超曲面是全测地的。
中的完备极大类空超曲面是全测地的。
正象Marden和Tipler指出的那样,对任意时空中常平均曲率完备类空超曲面在相对论中都有意义。因此完备类空超曲面的研究近年来迅速发展起来。
从1987年~1991年Akutagawa、成庆明、Ramanathan的结果可归结为:
定理13 设M是de Sitter空间 中的n维具有平行平均曲率向量的完备类空子流形。如果n2H2≤4c(n=2)或n2H2<4(n-1)c(n≥3),则M是全脐的。
中的n维具有平行平均曲率向量的完备类空子流形。如果n2H2≤4c(n=2)或n2H2<4(n-1)c(n≥3),则M是全脐的。
另外应该注意的一个问题是洛仑兹空间形式的完备类空子流形和黎曼空间形式中的常平均曲率的完备子流形有个本质的区别,即黎曼空间形式中的第2基本形式中的模长平方可能是无界的,但洛仑兹空间形式的常平均曲率的完备类空子流形的第2基本形式的模长平方一定是有界的。这已经被成庆明和Nakagawa证明。
并且这类超曲面的一些特征也已经被给出。类空子流形的研究主要是80年代开始,今后将会有更大的发展。
。【参考文献】:1 Simons J. Ann of Math, 1968,88:62~105
2 Bombieri E,et al. Invent Math,1969,7:243~268
3 Chern S S, et al. Functional analysis and related fields. Berlin -New York:Springer, 1970,59~75
4 Yau S T. Amer. J Math, 1974;96:346~366,1975,97:76~ 100
5 Cheng S Y, et al. Ann of Math,1976,104:407~419
6 Peng C K, et al. Seminar on minimal submanifolds,Princetin Univ. Princeton,1983,177 ~198
7 杨 洪苍,等.科学通报,1990,34:167~171
8 Cheng Q M.Math Z,1991,206:333~339
(东北大学成庆明撰)