工程结构流变问题
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第182页(3950字)
工程结构的流变问题是流变学在工程结构中的应用。
工程结构的蠕变现象在19世纪已观察到,但它的真正性质到本世纪初才发现。1907年美国材料试验学会(ASTM)首先报导了钢筋砭梁的蠕变资料。1910年E.N.Ha Andrede首先揭示了金属蠕变三阶段概念。到本世纪30年代,关于工程结构的蠕变现象、特性和基本理论大体形成,以后又进一步发现应力松弛现象。
从20世纪30年代至今的60年中,有关砭结构与金属结构等的流变问题取得巨大进展,现已查明,砭结构在不变持续荷载作用下,变形随时间不断增长,其数值可达瞬时弹性变形的1~3倍。在预应力钢筋砭结构中,由于应力松弛引起预应力逐渐丧失的现象。
而且由于流变,结构中的应力应变状态也为之改观,因此,在结构设计中,流变是个不可忽视的因素。以下简要介绍若干工程结构的流变问题。
线粘弹性梁 前捷克斯洛伐克Zdenek Sobatkm提出了等价应力,等价应变等一系列有关概念,并把微分型和积分型合并,抽象出微分-积分算子概念,对工程结构粘弹性体进行了系统的研究,导出了一系列新结论。
由于引进了“等价”概念,普遍虎克定律仍成立。

 ,
,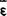 分别称为等价应力和等价应变。
分别称为等价应力和等价应变。
E0(x,y,z,t)-普遍弹性模量,它与坐标及时间有关。
定义微分-积分算子:

类似地定义:等价曲率  等价挠度
等价挠度  等价弯矩
等价弯矩  等价剪力
等价剪力  等价荷载
等价荷载  对于粘弹性梁,假定“平面假设”仍成立,于是有
对于粘弹性梁,假定“平面假设”仍成立,于是有

式中,C-曲率,W-挠度。由(1)、(5)式,有

由材力知

两端作用算子Ã,则

式中 ,对质心的惯性矩,F-横截面。
,对质心的惯性矩,F-横截面。
由(6),(7)得

与受纯弯曲的弹性梁的正应力公式有相似形式。
对于弹性梁,弯矩、剪力、荷载有如下关系:

两端分别作用算子Ã,则得

(7)式代入(9)第三式,得

与弹性梁结果类似。
线粘弹性刚架 粘弹性刚架的转角和位移的有关公式,如弹性刚架一样可借助虚功原理导得。
在弯矩M作用下弹性杆单元ds的转角为

结合(1)、(5)、(8)式可导得粘弹性杆单元的等价微分转角为

定义
等价转角 
等价轴力 
等价扭矩 
等价扭角 
把 、
、 看成虚值,直接应用虚功原理,或先对W、dφ应用虚功原理,然后作用以算子
看成虚值,直接应用虚功原理,或先对W、dφ应用虚功原理,然后作用以算子 均可得
均可得

把(11)式代入,得

式中M0及后文将用到的Q0、.Nt、Mt0分别表示在所求位移方向作用的单位力引起的弯矩、剪力、轴力和扭矩。
应用虚功原理,类似地可得由等价剪力引起的等价位移(挠度)

式中k为剪应力分布不均系数,G0为普遍剪切模量。
类似地,可得由等价轴力引起的等价挠度,等价扭矩引起的等价扭角。
于是,由等价弯矩、剪力、轴力、扭矩 、
、 、
、 、
、 引起的总等价位移为
引起的总等价位移为

(15)
线粘弹性板
定义:
等价应力分量 
等价应变分量 
线性各异体向性的等价应力-应变关系为

式中Cijkl(x,y,z,t)为各向异性普遍四阶张量。
由弹性薄板理论知
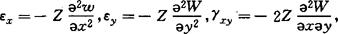
引用张量,偏导数下标记法,记为

作用以算子 ,有
,有
 (17)
(17)
代入(16)式,则有

由弹性理论知,单位长度板的弯矩可表为

弯矩平衡方程的张量表达式为
mij,ij=-q(x,y,t)
即

对它们分别作用以算子Ã,则有

若沿板厚各向一致异性,将(19)连(18)式代入(20)式,则得

对于均匀厚度一致正交板,则有

与弹性薄板受横向荷载弯曲时的位移方程

有类似形式。
线粘弹性壳 考虑-薄壳单元,由力的平衡,得3个平衡方程,并分别作用以算子Ã,得粘弹性薄壳的等价平衡方程如下:

式中 、
、 、
、 分别为x、y、z轴方向的等价荷载分量;
分别为x、y、z轴方向的等价荷载分量;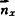 、
、 、
、 分别为法向和切向等价合力分量;
分别为法向和切向等价合力分量; 、
、 、
、 分别为等价弯矩和扭矩。且
分别为等价弯矩和扭矩。且

等价应力合力分量和等价应力合力偶为

式中,当i=j时,分别为 ,
, ,
, ,
,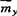 ,
,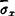 ,
, 。
。
S是局部坐标,表达任意点到薄壳中性面的垂直距离。
妨弹性理论,可得等价应力、应变关系的物理方程,等价应变、位移关系的几何方程。忽略法向应力及剪应力对垂直于中性面方向的变形的影响,对一致正交的粘弹性壳有:

式中 、
、 、
、 、分别是x、y、z方向的等价位移分量。z=z(x,y)是中性面方程。
、分别是x、y、z方向的等价位移分量。z=z(x,y)是中性面方程。
且 ,
, ,
, ,
,
(26)连同(27)式分别代入(24)、(25)式,得 ,
, ,再代入(23)式,乃得基本微分方程组:
,再代入(23)式,乃得基本微分方程组:

式中 ,
, 是复杂线性微分算子,例如
是复杂线性微分算子,例如

以上介绍,借助微分一积分算子及等价变量概念,推导粘弹性梁、板、壳的若干主要结果的一般方法。其实,对每种结构,可根据实际材料的流变特性及其流变模型,直接推导具体本构关系。
我们仅就线粘弹性体而论,对于非线性粘弹性体,也可得出相应方程,只是形式更为复杂。
。【参考文献】:
1 Ponter A R S, Hayhurst D R. Creep in Structures, 3rd IU-TAM Symposiuin, Leicester, UK, 1980
2 Spinger - rerlag Berlin Heidelterg New York,1981
3 Zdeněk Sobatka. Rheology of Materials and Engineering Structures, ACADEMIA Prague, 1984
4 Irving H. Shames, Elastic and Inelastic Stress Analysis Prentice-Hall, Inc. New Jersey, 1992
5 Reiner M. Deformation, Strain and Flow, The Whitefriars Press Ltd. , 1960
(上海城市建设学院陈德坤教授撰)