Bers空间中之逼近
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第44页(3822字)
设D是扩充复平面C上其边界 至少含2个点的单连通区域,从而D共形等价于单位圆盘
至少含2个点的单连通区域,从而D共形等价于单位圆盘 。
。
不妨令ψ是就范于ψ(ξ0)=0,ψ′(ξ0)>0的D到△上的共形映射,而ψ-1为其逆映射,此处ξ0∈D是固定一点,置λD(ξ)|dξ|为D上的Poincare度量。若用A(1)表示D上的解析函数之全体,那么时于p∈(0,∞)我们可用Poincaré度量定义D上的Bers空间 (D),它是由满足
(D),它是由满足 <∞的函数f∈A(D)组成的完备的线性空间。
<∞的函数f∈A(D)组成的完备的线性空间。 ,q∈[2,∞)首先是由L.Bers在1965年引入并开始研究的,它是着名的Hardy空间H1(△)的推广。
,q∈[2,∞)首先是由L.Bers在1965年引入并开始研究的,它是着名的Hardy空间H1(△)的推广。
后来,数学家把 ,q∈[2,∞)拓广到更一般的情形亦即
,q∈[2,∞)拓广到更一般的情形亦即 ,p∈(0,∞),q∈(0,∞)于是也就统称为Bers空间。Bers中的逼近论主要是指:Bers空间中多项式类的完备性;Bers空间中的多项式之最佳逼近问题;Bres空间中的有理函数之逼近各分支在实际中,如在物理学的电场理论中,都有重要的意义。以下主要从3个方面来综述。
,p∈(0,∞),q∈(0,∞)于是也就统称为Bers空间。Bers中的逼近论主要是指:Bers空间中多项式类的完备性;Bers空间中的多项式之最佳逼近问题;Bres空间中的有理函数之逼近各分支在实际中,如在物理学的电场理论中,都有重要的意义。以下主要从3个方面来综述。
(1)Bres空间中多项式类的完备性。设 及
及 。
。
不难知道tD∈[1,2]而I(1)=(1,∞)及I(2)=[2,∞)。这2个量是J.Burbea于1977年引进的。它在多项式类于Bres空间中之完备性研究中起着很重要的作用。1934年,А.И.Mapкyшeвиy与O.J.Farell独立地证明:若D是Caratheodory区域,则多项式类在 ,p∈(0,∞)中是完备的。
,p∈(0,∞)中是完备的。
接着,在1966年和1969年L.Bers和M.J.Knopp分别将他们的结果推广到D为Jordan区域时的 ,q∈[2,∞)上去了。又若对区域D的条件加强,即当D是CмиpHов区域时,T.A.Metzger与M.Sheingorn在1973年证实了多项式类在
,q∈[2,∞)上去了。又若对区域D的条件加强,即当D是CмиpHов区域时,T.A.Metzger与M.Sheingorn在1973年证实了多项式类在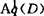 ,q∈(1,∞)中是完备的。
,q∈(1,∞)中是完备的。
其实,M.Sheingorn对一类特殊的Jordan区域——早被J.Earle与A.Marden定义,证明了上述事实。如 是可求长的Jordan曲线,那么T.A.Metzger就
是可求长的Jordan曲线,那么T.A.Metzger就 和q∈(1,∞)分别于1973年和1974年证明了多项式类在
和q∈(1,∞)分别于1973年和1974年证明了多项式类在 中完备。进而,如(ψ-1)′(△)是C上可以忽略一个正对数容量集,那么就q∈I(tD)多项式类还在
中完备。进而,如(ψ-1)′(△)是C上可以忽略一个正对数容量集,那么就q∈I(tD)多项式类还在 中完备。从上面的若干结论看出,一旦限制区域D的条件愈多且要使多项式类在
中完备。从上面的若干结论看出,一旦限制区域D的条件愈多且要使多项式类在 中完备,那么对q的限制也就愈少。
中完备,那么对q的限制也就愈少。
于是,自然会问:是否可以同时减弱D及q的条件使多项式类仍在 中甚至在
中甚至在 中完备呢?J.Burbea做了这方面的尝试。他在1977年获得如下结果:当D是Jordan区域且ITD=1时,那么多项式类在
中完备呢?J.Burbea做了这方面的尝试。他在1977年获得如下结果:当D是Jordan区域且ITD=1时,那么多项式类在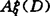 中完备,其中p∈(0,∞)且q∈I(tD)。
中完备,其中p∈(0,∞)且q∈I(tD)。
同年,他对D是Caratheodory区域得到相同的结果。后来J.Burbea在J.Brennan的提醒下于1978年考虑了D为非Cartheodory区域时多项式类在 中之完备性,得到类似的结论。
中之完备性,得到类似的结论。
(2)Bers空间中多项式之最佳逼近。换句话是,多项式类在 中的逼近阶估计及其逆定理之问题。
中的逼近阶估计及其逆定理之问题。
为此,对 及δ>0先令
及δ>0先令 ,ω(δ,f)=sup{‖f(*+h)-f‖(p,q,△):|h|≤δ}并规定
,ω(δ,f)=sup{‖f(*+h)-f‖(p,q,△):|h|≤δ}并规定 。其次,若用
。其次,若用 表示所有次数不超过n的代数多项式Qn组成的集合,则置
表示所有次数不超过n的代数多项式Qn组成的集合,则置 。从1984年到1989年,沈燮昌、邢富冲及苏兆龙研究了
。从1984年到1989年,沈燮昌、邢富冲及苏兆龙研究了 ,p∈(0,∞),q∈(1,∞)中的多项式类之最佳逼近问题,他们3人获得:
,p∈(0,∞),q∈(1,∞)中的多项式类之最佳逼近问题,他们3人获得: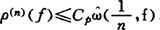 ,进一步,若
,进一步,若 则ρ(n)(f)≤
则ρ(n)(f)≤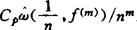 。这儿,Cp>0是一仅依赖于p的常数,又当p∈[1,∞)时,有
。这儿,Cp>0是一仅依赖于p的常数,又当p∈[1,∞)时,有 ,C>0为一常数。
,C>0为一常数。
同时,他们又给出上述结论的逆命题。此外,1987年,沈燮昌、邢富冲与张有光获得了 ,p∈(0,1),q∈(1,∞)中的Hardy-Littlewood型不等式并用于逼近。
,p∈(0,1),q∈(1,∞)中的Hardy-Littlewood型不等式并用于逼近。
就一般区域D,钟乐凡用Faber变换于1988年证明了:若 是光滑曲线且其切线与正实轴的夹角满足Lipα,α∈(0,1)条件,那么,就
是光滑曲线且其切线与正实轴的夹角满足Lipα,α∈(0,1)条件,那么,就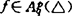 ,q∈(1,∞)有
,q∈(1,∞)有 当且仅当
当且仅当 。次年,钟乐凡利用邢富冲和苏兆龙之定理又给出了当D是含原点的Lipschitz区域时
。次年,钟乐凡利用邢富冲和苏兆龙之定理又给出了当D是含原点的Lipschitz区域时 在
在 ,p∈(1,∞),q∈(1,∞)中的逼近阶。
,p∈(1,∞),q∈(1,∞)中的逼近阶。
(3)Bers空间中的有理函数之逼近,这类问题通常比前两类难得处理。首先,L.Bers在1965年证明如下事实:若 且
且 是Ample的,则对任意的
是Ample的,则对任意的 都存在极点只在∧上的有理函数Rn使得
都存在极点只在∧上的有理函数Rn使得 。特别考虑形如Sn
。特别考虑形如Sn ,
, 的有理函数在
的有理函数在 中的逼近问题是很有意思的,因为1/(ξ-ξk)可以看成点ξk处有单位电子引起的复电场。1973年,C.K.Chui证明了:若D是Jordan区域且
中的逼近问题是很有意思的,因为1/(ξ-ξk)可以看成点ξk处有单位电子引起的复电场。1973年,C.K.Chui证明了:若D是Jordan区域且 可求长,则
可求长,则 ,q∈(2,∞)可被形如Sn(ξ)的有理函数逼近,即
,q∈(2,∞)可被形如Sn(ξ)的有理函数逼近,即 。
。
1972年,D.J.Newman指出q∈(2,∞)是必不可少的,他还指出:当q∈(1,2]时, ,在
,在 中不可能被形如Sn的函数逼近。一般地,C.K.Chui与沈燮昌合作,在q∈(2,∞)下,对
中不可能被形如Sn的函数逼近。一般地,C.K.Chui与沈燮昌合作,在q∈(2,∞)下,对 加上一此光滑条件:
加上一此光滑条件: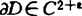 ,ε>0,获得了Sn在
,ε>0,获得了Sn在 中的逼近速度,亦即En,q(S)=sup{inf{‖f-Sn‖(1,q,D)∶sn}:Sα}=0(1/nq-2)或O
中的逼近速度,亦即En,q(S)=sup{inf{‖f-Sn‖(1,q,D)∶sn}:Sα}=0(1/nq-2)或O ,此处
,此处 。
。
更深入一步,他俩还得到f具有高阶导数时的逼近阶的精确估计。再者,对于给定极点在区域外部的有理函数在Bers空间中的逼近问题,1987年,先由沈燮昌同吴志坚合作获得:设 且sj为αj在{αk}i中出现的次数,若
且sj为αj在{αk}i中出现的次数,若 ,ε>0,β∈R1,则对
,ε>0,β∈R1,则对 ,p∈(1,∞),q∈(1,∞)存在
,p∈(1,∞),q∈(1,∞)存在 使得
使得 当且仅当
当且仅当 αj|)=∞进而,若不假设
αj|)=∞进而,若不假设 位于上述角形区域,则为了实现上述逼近,就只须将
位于上述角形区域,则为了实现上述逼近,就只须将 改成
改成 即可。
即可。
到了1988年,C.K.Chui和沈燮昌把沈-吴之结果推广到△上的比Bers空间更为广泛的空间Ap(φ),p∈(1,∞)上去了。最后,肖杰于1990年研究了再生核型有理函数序列在Ap(ψ),p∈[1,∞)上去了。最后,肖杰于1990年研究了再生核型的有理函数序列在Ap(φ),p∈[1,∞)中的逼近,而相应于 ,p∈(1,∞),q∈(1,∞)中的结果分别由S.Axler、D.H.Luecking和R.Rochkerg等人在1980~1986年之间获得。沈燮昌和肖杰又把肖杰的结果推广到一般的Bers空间
,p∈(1,∞),q∈(1,∞)中的结果分别由S.Axler、D.H.Luecking和R.Rochkerg等人在1980~1986年之间获得。沈燮昌和肖杰又把肖杰的结果推广到一般的Bers空间 ,p∈(1,∞),中去了。
,p∈(1,∞),中去了。
以上是自20世纪60年代以来关于Bers空间中各类逼近问题的一个基本又是主要的概述。研究这些问题的数学家主要是采用实分析、复分析、调和分析、泛函分析、函数构造逼近及数值计算等方法进行讨论的。其实,在这一领域还存在大量的问题值得研讨。(1)对于不同特征的区域,究竟赋以什么度量性的充要条件才能使多项式类在 中完备?这个问题的解决是否会与区域的某种“容量”有关。
中完备?这个问题的解决是否会与区域的某种“容量”有关。
(2)就多项式的最佳逼近论中,考虑f∈ 具有高阶导数情形以及当p∈(0,∞),q∈(0,1)时一般Bers空间
具有高阶导数情形以及当p∈(0,∞),q∈(0,1)时一般Bers空间 中多项式最佳逼近。此外能否将已知结果中的区域之边界条件进一步减弱也是值得考虑的问题。(3)在一般区域D上或D上或
中多项式最佳逼近。此外能否将已知结果中的区域之边界条件进一步减弱也是值得考虑的问题。(3)在一般区域D上或D上或 上找插值基点以及由其产生的插值多项式,如Lagrange,Hermite,等插值多项式使得它们在
上找插值基点以及由其产生的插值多项式,如Lagrange,Hermite,等插值多项式使得它们在 中进行逼近,并求出逼近阶。(4)讨论极点在区域D的边界
中进行逼近,并求出逼近阶。(4)讨论极点在区域D的边界 上的一个子集∧的有理函数在
上的一个子集∧的有理函数在 中的完备性是重要的。另外,研究再生核型的有理函数类(极点在D的外部)在
中的完备性是重要的。另外,研究再生核型的有理函数类(极点在D的外部)在 中的完备性也是极为有意义的,因为它与现代的调和分析理论和插值论紧密联系在一起的。(5)试把前述的一切概念,思想与方法,理论,结果与问题全部移植到多连通区域上的Bers空间中去并找到它们在其它学科中的应用是非常有意义并富有创作性的工作,但这不是一件容易的事。
中的完备性也是极为有意义的,因为它与现代的调和分析理论和插值论紧密联系在一起的。(5)试把前述的一切概念,思想与方法,理论,结果与问题全部移植到多连通区域上的Bers空间中去并找到它们在其它学科中的应用是非常有意义并富有创作性的工作,但这不是一件容易的事。
1 MapicyuieBHy A и.TeopияaHaпTичeekиx фyHKчий rиTTL MOCKBa-пeHиHrpag,1950
2 BersL. J Analysis Math, 1965,14:1~4
3 Bers L. Amer,J Math, 1965,87:196~214
4 Bers L. Acta Math,1966,116:113~134
5 Chui C K. Proc AmerMath Soc,1973,40(2):438~442
6 Burbea J.J London Math Soc,1977,15(2):255~261
7 Burbea J. Ark Math,1978,16:229-234
8 沈燮昌.复变函数逼近论.北京:科学出版社,1992
9 肖杰.北京大学理学博士论文,1992
10 钟乐凡.数学年刊,1992.13A(4)∶465~472
(北京大学沈燮昌教授、肖杰博士撰)