系统评价方法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第258页（4569字）

系统分析的核心，是通过构造系统模型来了解系统的本质和规律。一旦系统设计完成之后，就要以适当的方法对它进行评价。所谓评价，就是根据明确的目的来测定对象的属性，并将属性变为主观效用的行为。因此，在评价时，首先要有明确的目标，然后从评价的目标规定评价对象，并测定其功能、性能和由其所产生的影响等的属性。

在开发系统时，评价环节是非常重要的。如果评价不当，不仅设计的系统难以实现，而且还要付出庞大的费用。因此，在开发阶段，要给定系统目标和最佳方案，以及决定与效果相称的费用等。评价的方法有多种，下面予以扼要的介绍。

1．相关矩阵法

相关矩阵法，是在评价系统要素，加从若干可行方案中选择某几个时，在这些方案相互之间无干涉情况下所使用的一种评价方法。如表2．1．7－1所示，有评价因素(可行方案A、B、……)a、b、c、……，并就评价因素(评价观点，如可靠性、价格、操作性……)A、B、C、……进行评价时，如各因素的相对加权值为W_j，对各评价项目的评价因素的评价值(如对量和质给定分数和加权值)取a_ij时，并以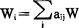作为各评价项目i的全部评价值W_i，那么，就可以根据这个值的大小按顺序进行排列。系统评价的实例如图2．1．7－1，其评价因素有功能、费用、时间(工期、交货期、寿命等)和可靠性等，加权量分别为W₁、W₂、W₃、W₄。

表2．1．7－1 相关矩阵表

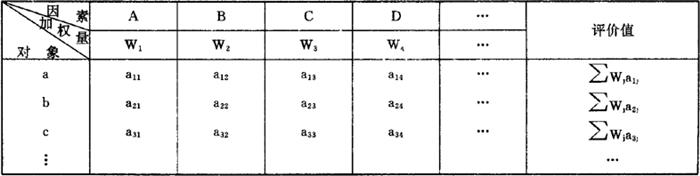
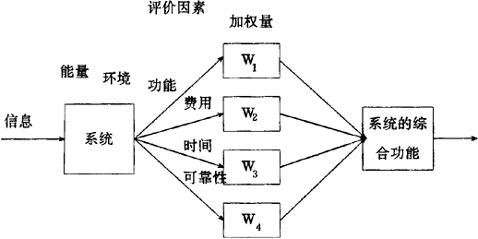
图2．1．7－1 系统评价

2．交叉增援矩阵法

交叉增援矩阵法，是在评价要素和评价对象间有相互干涉时，对其评价结果进行修正的一种矩阵方法。采用这种方法对评价结果进行修正时，可将相关矩阵法所得的评价值W_i乘100加以标准化，其结果W_iN可用下式表示：

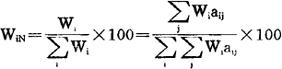
考虑各项目间的相关程度，用β_ij表示由于j的产生而对i带来的影响。一般，β_ij≠β_ji，这时i和j都是评价项目。当j的产生对i的产生起促进作用时，用“+”号表示，起抑制作用时用“－”号表示。根据相关的程度，可对β_ij取1、2、4、8的指数函数值。

用上述的β_ij代替最初的评价值W_iN，并考虑到新的评价值W_iN时，则可变成下式：

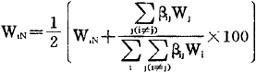
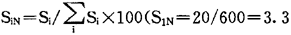上式右边的第一项是考虑各项目独立时的最初评价值，第二项是由于相互干涉产生的评价值。例如，表2．1．7－2所列的a、b、c、d四个评价对象，其最初的评价值W_iN被给定为20、30、40、10，相关度β_ij给定为β₁₂=2，β₁₃=－2，β₁₄=4，β₂₁=0，β₂₃=8，……时，就可对各项目计算S_iij=β_ijD_i，即S₁₂=2×30=60，S₁₃=－80，S₁₄=40，S₂₁=0，S₂₃=320，……。并可求得各项目i的相关度，S₂=340，S₃=40，S₄=200)。如将这些值乘100进行标准化，则可得到，S_2N=56．6，S_3N=6．6，S_4N=33．3)。该值与W_iN的平均值W_iN+S_iN)／2就是对各项目给出的新评价值NNW。

表2．1．7－2

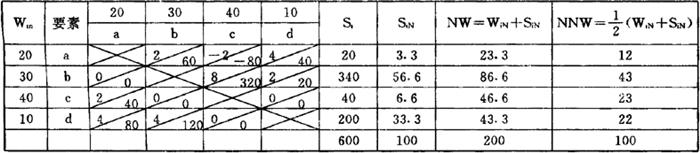
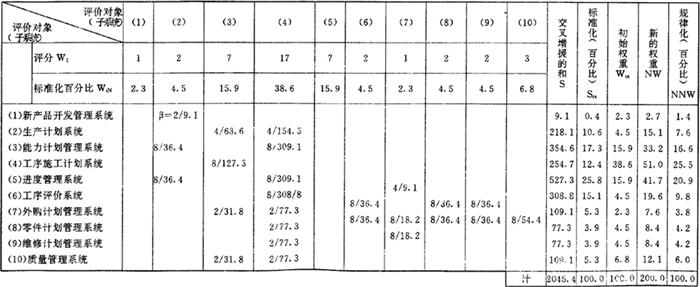
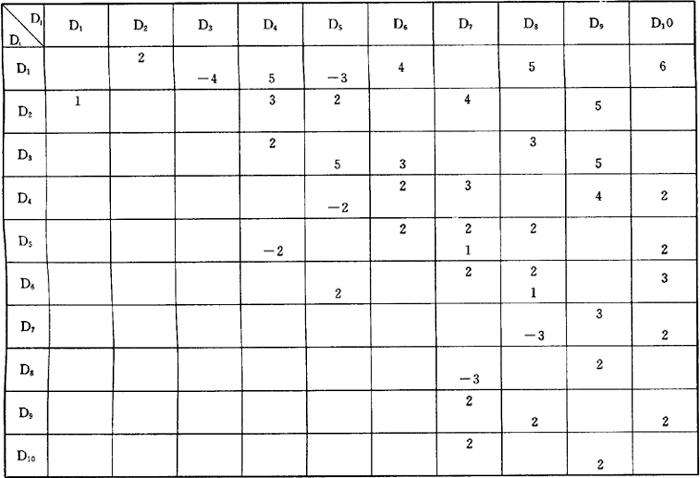
数值例如表2．1．7－3。考虑某生产系统时，对构成该系统i的子系统的重要性进行评价。利用相关矩阵法进行评价的值W_iN，各子系统间的相关度，象以NNW表示的值那样，改变着子系统的重要性。

表2．1．7－3 子系统间的交叉增援矩阵

3．交叉影响矩阵法

这是从技术之间的相关性出发，抓住未来的技术开发目标，对全部技术的展开进行分析的一种方法。它是在预测某一项目的发生概率时，对同其他预测事项之间存在的相互作用进行判断，并参照这种判断对即将预测事项的发生概率进行修正的评价方法。

在这种方法中，需要考虑相互间的相关强度(已实现的某个项目或尚未实现的某个项目对其它项目的影响程度)和相关模型(根据初始事项的发生，改善第二事项的发生概率或为了实现第二事项而要求进一步努力的促进式模型)，并根据初始事项的发生，减少以后事项的发生概率，或不让以后事项实现所需要的抑制式模型，以及无关的模型和扩散时间(即在某个项目实现或末实现之后，到接受其它项目的实现概率或影响所需要的时间)的问题。

对于事项D₁、D₂、…D_m及其发生的概率P₁、P₂、…P_m来说，假如令P_n为D_m未出现时的发生概率，P′_n为D_m出现后的发生概率，则有下式成立：

p′_N=f(P_n，M，S，t_m，t)

式中，M为相关模型的函数；S为相关强度；t_m为D_m的实现时间：t为将要进行预测的未来时期。

假如P′_n和P_n的关系为二次式，则

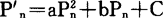
如令P_n=0，则P′_n=0；若令P_n=1，则P′_n=1。从这样的条件出发，上式可变为

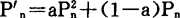
假如a为线性，则可用下式给出：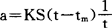

式中，K是由模型决定的值，可取－1或+1；S表示相关强度的系数，其值为O≤S≤1。

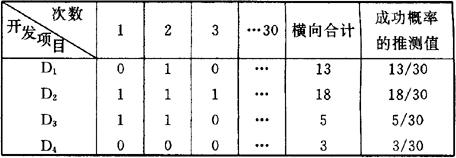
图2．1．7－2表示P′_n和P_n的关系的实现概率。图中的对角线表示无关系模型，对角线的上方各线表示促进式模型(－1＜a＜0)，对角线的下方各线表示抑制式模型0＜a＜1)。由P_n算出P′_n时，如考虑表2．1．7－4所示的开发项目及其初期概率，则可以此为基础对各项目制成概率(P)表2．1．7－5、交叉影响矩阵(CIM)表2．1．7－6和成功失败(SF)表2．1．7－7。计算P′_n的顺序为：第一步，从P表的D₁中任意选出其中的D_k(这里的K=2)。第二步，由概率P_k模拟发生的事项(以P₂=0．2试验D2的成功或不成功)。第三步，如成功则将P表和SF表的P₂作为1，并根据CIM表通过从P_n到P_n的变换式对P₁、P₃、P₄进行变换；不成功，就以P₂为0，P₁，P₂，P₄，无变更。第四步，将剩下的D₁、D₃和D₄按第三步修正的概率对事件的发生进行模拟，使P表的全部项目按第三步的顺序变换到0或1，然后将其计入SF表中。第五步，使第一步到第四步的顺序返复N次，将其结果S_ij(i=1－4，j=1－N)记入SF表中。第六步，将SF表中横向合计用N除得的值表示D_j的成功的概率。

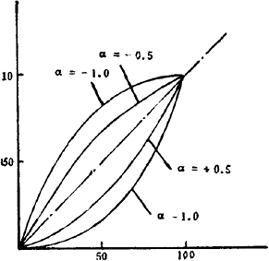
图2．1．7－2 实现概率

表2．1．7－4

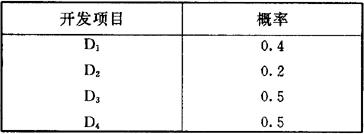
表2．1．7－5

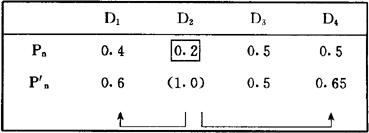
表2．1．7－6

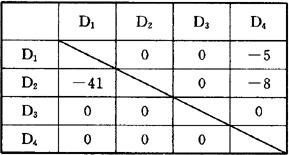
表2．1．7－7

4．修正交叉影响矩阵法

各项目之间的影响程度，随着项目P_j的实现时间的不同，在项目P_j预测时间前的位置亦有所不同，特别是复合项目的影响比单一项目的影响要复杂。为了弥补交叉影响矩阵法的不足，因而提出修正交叉影响矩阵法。这种方法是把项目D_j成功的时间t当作概率变量来考虑的。其概率密度函数对于D_j来说，是由作为社会需要、研究费用和技术的难易程度等函数决定的。成功的概率以图2．1．7－3(a)中斜线面积表示。由于D₁的成功而引起D_j成功概率的增加，并随着位置的变化，则密度函数的形式也跟着变化，如图2．1．7－3(b)所示。

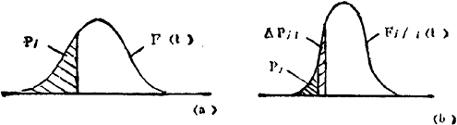
图2．1．7－3 D_j在成功瞬时点上的概率分布

在预测开发项目D_j的成功时期时，假定初期分布函数为F_j(t)，如果从t=0到t=t₀之间D_j没有成功，并且与D_j相关的其他研制项目也没有成功，而t≥t₀的分布函数F_j(t，t₀)如果可用下式给出，即

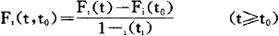
则D_j从t=t₀到t=t₀+△t之间成功的概率为

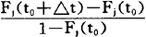
另一方面，t_j初始分布函数F_j(t)的预测，可用PERT(计划评审技术)的时间预测法进行。即

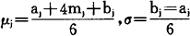
那么，影响D_j的开发项目在D_j成功以前成功时，即P₁在t=t_j中成功时，如果令t≥t₁的分布函数为F_1／1(t，t_i)则分布函数可用于式表示。

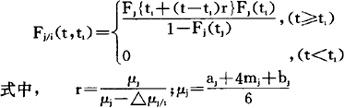
当开发项目为D₁、D₂、……多个时，由于这些项目的成功，对D_j的综合效果来说，可分为根据社会的需要提出的△μ_j／i(N)和从技术上考虑的△μ_j／1(T)来评价求解。例如，有10个开发项目，并令其时间间隔△t为一年，则各开发项目的a_j、m_j、b_j可由表2．1．7－8算出。利用表2．1．7－9，以△μ_j／i(T)为上段，△μ_j／i(N)为下段，对D_i给D_j的影响进行1000次模拟，就可得到D₁出现的次数

表2．1．7－8 各开发项目的预想年

表2．1．7－9 D_i给D_j的影响

5．费用效果分析法

这是根据系统的效果和费用的分析结果，对系统进行评价的一种方法。其构成如图2．1．7－4。它主要是决定目标尺度和环境的定量比，以及同系统特性和环境特性的目的尺度结合问题。另外，在对代替方案进行评价时，还要充分考虑难以定量化的不确定性因素。为此，在这种分析方法中，主要分析的问题是：(1)系统的目标是什么?(2)提案系统何时可以使用?(3)系统达到目的的程度如何?(4)系统的开发和运行费用需要多少?(5)实现系统目标的最优策略是什么?(6)在预定的系统特性或估计的费用中，所包含的风险或不确定因素是什么。

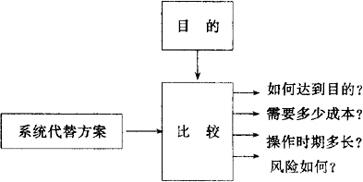
图2．1．7－4 费用与效果分析