正交实验设计

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第358页（7929字）

单因素和双因素的实验设计与方差分析是以因素和水平的全组合逐一并重复的实验方式，故称之全面实验。当因素多于2个后，采用全面试验的方法，其工作量将随因素的个数按指数方式剧增。这种大工作量的实验既不经济，又延误时间。一个好的实验设计应该是使其效率优于当前生产，使其结论早于当前生产。如何优化多因素的实验就是正交设计研究的目标。

1．拉丁方与正交表

(1)拉丁方的由来与演变

早在十八世纪，Euler提出了一个有趣的数学问题，要求分别来自六个师团的6种不同军衔的36名军官，排成一个6×6的方阵，并且每行每列都有6种军衔和6个师团的军官，这就是着名的36军官问题。解题的思想是用不同的拉丁字母A，B，C……表示军官，希腊字母α，β，γ……表示团队，拉丁字母和希腊字母各组合成序对占据每一个行列的交叉位置，构造成一个方阵，所以后来人们称这类问题为希腊拉丁方，简称为拉丁方。由于拉丁字母个数有限，必须要与相应的脚标联用，后来只用阿拉伯数字代替拉丁字母。所谓n阶拉丁方是指自然数1，2，…，n的每一个数字在方阵中的每一行和每一列上只出现一次的阵列。设A=(a_ij)_n×n和B=(b_ij)_n×n是两个n阶拉丁方，如果并置方阵N=(a_ijb_ij)_n×n中的n²个序偶各不相同，用向量表示A×B=(a_ijb_ij)=0则称A和B正交，称序偶方阵N为正交拉丁方。直到1901年G·Tarry才证明实现36军官的正交问题无解，但是又过了大约半个世纪，在第二次世界大战后许多国家的学者借用拉丁方的构造原理解决了多因素实验优化设计的问题，从而大大加速了试验过程，有力地促进了工农业生产的发展。

多因素实验所需解决的问题不外乎是：

①查明各因素对实验指标的影响，即分清主要因素和次要因素，区分独立作用因素和交互作用的因素。

②找出因素中最佳水平的组合，形成最优生产条件，必要时可以对生产过程给出预报信息。

除此之外，要求设计的实验方案不但力求减少实验的操作次数，还应使每种因素的各个水平都能在实验过程中显示出作用。为此，利用参加实验的因素拉丁方和水平数的拉丁方并置成由有序组构成的正交实验拉丁方，使得各个因素的各个水平的搭配(是有序组，但不是全组合)都能进行实验，这种安排实验的方法称为正交实验设计。

(2)正交表

当因素和水平较多时，利用正交立方体选取搭配点就显得十分不方便。为此，人们根据正交设计的思想。运用数学方法，将正交实验中各种因素和水平搭配的结果编制成表格，称这一套规格化的表格为正交实验设计表，简称正交表。实验工作中，根据需要选择相应的表格作为实验方案。

已经规范化的正交表常用符号L_k(P^J)表示，如L₃(2³)，L₉(3⁴)等，其意义是

L——表示安排实验方案的正交表；

K——表示实验方案个数，即具有K个不同的各因素水平的组合，为正交表的行数；

P——表示参加实验因素的水平数；

J——为正交表的列数，表示可安排因素的最多数目不能超过J。

例如L₂₇(3¹³)，表示有27个实验方案，每个因素的水平数等于3的13列正交表。

表4．3．4－1是L₉(3⁴)的内容，从中可以发现正交表具有以下两个特点：

表4．3．4－1 L₉(3⁴)正交表

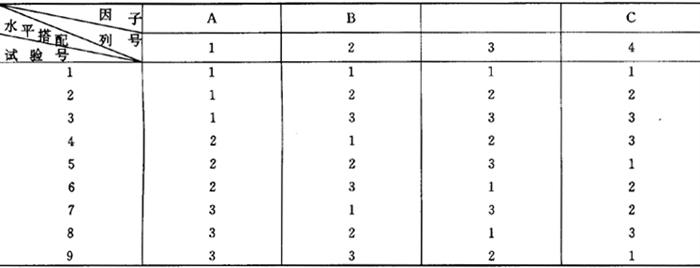
①任一因素占据一列位置，其不同的水平参加试验的次数都是相同的，如L₉(3⁴)中每列中1，2，3表示的三个水平都出现了3次；

②任两列不同因素水平所构成的序偶数相等，相同序偶数出现的次数在两列内的次数也相同。如{1，1}，{1，2}，{1，3}，{2，1}，{2，2}，{2，3}，{3，1}，{3，2}和{3，3}在每两列之间都出现了一次。

应当注意的是参加实验的因素如果不存在交互作用，所占据的列号可随意分配；有交互作用的因素则应按交互作用的设计来安排各个因素的位置。正交表的表头又划分为若干组，有一些试验必须按组分别安排因素及其交互作用列的位置。凡是单个因素占据的列号下的水平是实际参加实验的，没有单个因素占据的列号，所安排的水平是为计算交互效应或实验误差所设置的。因此行号表示实验方案的种类，每一行表示一种实验方案，该种方案是各因素所占据列号下所属水平的搭配。例如L₉(3⁴)中，如果因素A，B和C分别占据1，2和4列，第六行参加实验的因素水平搭配是A₂B₃C₂，而与第3列无关。

2．正交实验的特点

正交表提供了优选的实验方案，但并未解决最佳方案的问题，如何确定最佳方案，需要依据方差分析的结果。为了进一步揭示正交实验设计的实质，有必要首先认识其特点，以便于进行方差分析。

正交实验设计对实验因素与水平的安排具有均衡搭配和综合可比两个特点，因此能以少量实验取代全面实验，以节省实验的人力、物力和时间。

(1)实验方案的均衡搭配

如前所述，对于三因素三水平的对比实验，正交设计的优选结果是从27种有序方案中保留九种。这九种方案在正交表中安排为9行，每行为不同水平的有序组，称为一个实验条件，亦即一个实验方案。每一列表示一个因素不同水平的编号，使得各个水平出现的次数完全相同。尽管九次实验条件各不相同，但由于巧妙的安排使得三个因素的作用可以清楚地加以区分。由表4．3．4－1可见，在九种实验方案中，A，B，C三种因素的三个不同水平在这九次实验中各自参加了三次。同时，任何两因素水平的有序偶在全部实验中都能出现。这一安排就相当于双因素的交叉分配的全面实验，比如A₁B₁，A₂B₂，A₃B₃，A₁B₂，A₁B₃，A₂B₁，A₂B₃，A₃B₁，A₃B₂，这九种搭配分别参加了一次实验，没有重复，亦无遗漏。这种搭配表现为因素水平序偶的正交性和均匀性。对于多因素的正交实验，在n次实验中，每个因素的各个水平都参加了相同的次数，每两个因素的水平的各种搭配在n次实验中全部出现而且次数相等，具备这两个特点的实验设计就称为均衡搭配。

这种均衡搭配，特别是每两个因素之间的水平全组合在实验中全部出现，刻划出了用少量的经优选的方案反映全面试验面貌的可能性。同时，只有这种均衡的搭配使其实验结果的数据分析提供了依据，才能进一步确定最佳生产方案。

(2)实验指标的综合比较

均衡搭配是以部分试验代替全面的一种优化设计，欲区分各个因素对实验的影响则需利用正交表综合可比的性能。

综合可比的性能，是正交表所具备的第二个特点，利用行与列上有序组的不同与各水平出现次数相同的规律，采用筛选法和归类法来确定因素与实验指标之间的对应关系。具体地测试各次实验的指标数据后，计算各因素不同水平下实验指标的平均值。平均值的比较反映出各个水平对指标的影响大小及其程度，这种比较是同一因素下的水平对比。表4．3．4－2为一化学实验的二水平正交设计，不考虑其他因素，只要求计算由于催化剂A₁与A₂的不同对实验产品数量的影响。

表4．3．4－2 L₈(2⁷)

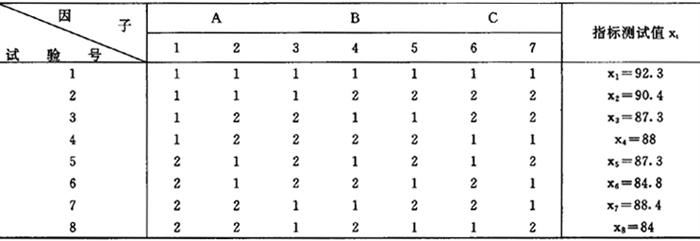
由表内水平搭配可知，将试验号1——4称为第一组，5——8称为第二组。在第一组中只有催化剂的水平A₁参加实验，在第二组中只有催化剂的水平A₂参加实验，而在两组之间其余因素B和C各个水平参加的次数完全相同，亦即在两组实验中其余因素对指标的贡献完全相等，计算两组的指标平均值

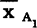与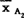的差值称做因素A₁与A₂的水平对比，显然是由于两种催化剂成分不同所引起的。这种对比排除了其他因素的影响，只反映因素A的水平改变对生产率所起的作用。就此而言，可以得出催化剂A₁比A₂好的结论。同理，可以作出其他因素的水平对比。正交表的设计正是在其余因素完全一致的情况下，对另一因素各个水平加以比较。利用各个因素水平得率均值对比的方法，就称为综合比较。

进行综合比较，不能脱离实验考查的具体对象。比如测试的实验指标，在某些对象中是数值越大越好，诸如热处理硬度和强度等，水平对比时，指标值越大越优，取对应指标平均值最大的水平就是该因素的最佳水平。相反在某些实验中指标值是越小越好，诸如材料的消耗与磨损等，水平对比时数值越小越优，取对应指标平均值最小的水平就是最佳水平。一般而言，因素从一个水平变化到另一个水平时，对应的平均指标值差距越大，则该因素对指标的作用灵敏度越高。对实验指标作用最灵敏因素称为主要因素。

由此可知，多因素的正交实验设计，是运用均衡搭配和综合可比的特性，将某一因素各水平下的试验指标数据分别求其均值加以比较。这一过程的实质就是化多因素问题为单因素实验问题进行分析和处理。所以正交实验是一个高效率的方法。

正交表L₈(2⁷)有8行7列，表明有可能安排7个因子，如果全面搭配需要做2⁷=128次实验，而利用正交表L₈(2⁷)只需做8次实验就可以代替全面实验的效果，实验效率提高了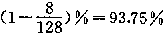．75%。同样，利用L₉(3⁴)，实验效率可达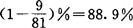。可见，利用正交表安排实验将显着减少实际操作时间、人力和物力。因此，正交设计是一个优化的实验方法。

3．正交表的构造方法

正交实验设计虽然具有均衡搭配和整齐可比的优点，但随着因素和水平数量的增多，计算工作量也随之增加。为了便于运用计算机编程对正交实验的结果进行分析，认识正交表的构造方法是十分必要的。

(1)有限域向量的加法和乘法

正交实验中涉及到的因素数和水平数随观察的具体对象不同而异。比如有2水平可安排7因子的L₈(2⁷)正交表，也有3水平可安排4因子的L₉(3⁴)正交表等等，其中水平数和因子数都是定义在有限数域中的。不同的水平数可用0，1，2，…，m表示，m是一个有限的自然数。这些有限水平数构成了一个集合，集合中元素之间又可以组成向量，比如U₂={0，1}。U₃={0，1，2}，…，U_i={0，1，…，t－1}分别表示二维，三维和t维不全为零元素的集合。

一个有限域至少应有两个元素，设U₂是由两个元素0与1组成的集合，元素之间的加法与乘法定义为

必须指出，向量U中各元素的加法和乘法运算与通常的代数运算是有所区别的，要求前者的和与积仍然属于该集合，否则必须修正。因为2不在U₂内，所以1+1≠2，而等于0。一般情况，U_t={0，1，2，…，t－1}，当元素间加法或乘法的结果不超出U_n的定义域，可按通常的代数运算取值，否则需要按下式修正其运算结果：设a，b，r∈U_n，则

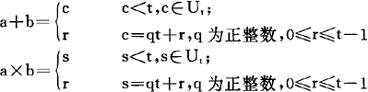
(2)独立向量的确定

定义：在集合U_t中，有不全为零的两个向量a=(a₁，a₂，…，a_m)和b=(b₁，b₂，…，b_m)。如果在U_t中找到一个不为零的元素a，即a∈U_t，使

a₁=ab_i，i=1，2，…，m

则称这两个向量是相关的；若a₁≠ab_i，则这两个向量无关，称a=(a₁，a₂，…，a_m)和b=(b₁，b₂，…，b_m)为独立向量。

例如，在U₃={0，1，2}中，共有九个二维向量：(0，0)，(0，1)，(0，2)，(1，0)，(1，1)，(1，2)，(2，0)，(2，1)，(2，2)。其中相互独立向量只有：(0，1)，(1，0)，(1，1)和(2，1)。由向量定义和加法、乘法可以证明a=(1，2)与b=(2，1)是相关的。

因2∈U₃，

则 a₁×2=1×2=2=b₁

a₂×2=2×2=4－1×3=1=b₂

故a=(1，2)与b=(2，1)是相关的，为非独立向量。

(3)正交表的构造方法

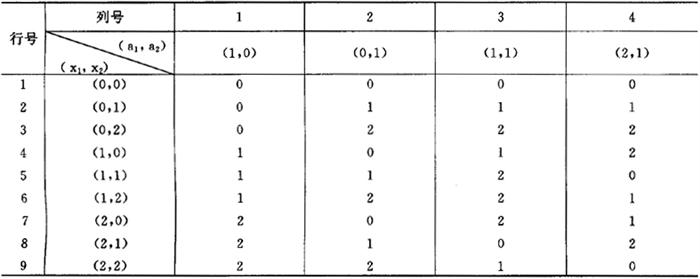
对于因素水平为t的正交实验，根据因素的多少来决定实验条件的规模，利用向量维数的取值不同来构造不同的正交表。在集合U_t={0，1，2，…，t－1}中，当维数为m时，以m维全部的向量依次作为正交表的行序，以m维中的独立向量作为列序。行和列向量之间依次对应相乘求积之和，将其计算结果加1后置于两向量所在行和列的交叉处，即为对应因素的水平数。

现以L₉(3⁴)表的构造方法为例，在U₃={0，1，2}中取m=2，二维向量共有9个，按顺序作为向量置于正交表的最左列，其中，独立向量有4个，依次置于正交表的最上面的一行各列中。行向量以(a₁，a₃)表示，列向量以(x₁，x₂)表示，则表中各水平数即对应行、列向量交叉处的数字为l_ij，则

l_ij=a_i1x_j1++a_i2x_j2

例如第一行第一列交叉位置的水平数字为

l₁₁=a₁₁x₁₁+a₁₂x₁₂=1×0+0×0=0

第二行第二列交叉位置的水平数字为

l₂₂=a₂₁x₂₁+a₂₂x₂₂=1×0+1×1=1

………………………………………………

第九行第四列交叉位置的水平数字为

l₉₄=a₉₁x₄₁+a₉₂x₄₂=2×2+2×1=(4－3)+2=3－3=0

现将各位置上的计算结果列于表4．3．4－3中，再将其中每一位置上的数字加1便成为表4．3．4－1的形式。同样的方式，选用m=3的向量运算法则可以构造L₂₇(3¹³)的正交表，依此类推可以构造各种规模的正交表。

表4．3．4－3 L₉(3⁴)的构造

(4)正交表的正确选用

充分利用正交表均衡性与可比性的特点，以参加实验的因素及其水平数为依据，选用恰当的正交表，力求达到实验次数较少，实验精度较高的优化设计。正确选择正交表应该遵循以下几个要求：

①水平数相符

对于等水平的实验设计，各因素的水平数都相等，即

P₁=P₂=…=P_n=P₀

其中n为实验因素的个数，P_n是第n个因素的水平数，如果选用的正交表为L_x(P¹)，且有

P=P₀

则满足水平数相符要求。对于不等水平的实验设计，由于实验因素的水平数一般都限制在两种范围内，所以可选用相应的混合水平正交表，即使没有现成的混合正交表，也可以对规格化的正交表进行改造，改造后的正交表各列自由度之和应等于改造前正交表各列自由度之和。总之选用与因素水平数相符的正交表是多因素实验设计的第一步。

②列数容限要求

正交表的列数J必须能容纳全部实验因素，因为一个因素要占据正交表的一列位置。对于L_k(P^J)，在不考虑交互作用时，必须有

J_min≥n

如果因素两两之间还有交互作用，全部列间交互作用的对数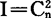。同样，每一交互作用对也应占据正交表的一个列位置，于是有

J_mi_n≥n+I

当然不一定两两因素间都存在交互作用，所以交互作用的对数Ⅰ应根据实际需要取值。如果把因素和因素之间的交互作用统称为实验因子时，在保证容纳全部因子的前提下，应当选用列数最少的正交表，即J_min称为满足容限要求的最小列。

应当指出，最小列J_min正交表仍然可能存在空列，以多余空列用来计算实验误差甚至比重复实验更为经济。

③满足行数要求

在m维向量中，每一向量占据正交表的一行位置，每行表示一个实验条件。m维向量的总数为K，独立向量数为J。由正交表的构造方法可知，K就是正交表的行数，J为正交表的列数，当实验因素的水平数确定后，K=P^m就是确定值，所以正交表的行数K与水平数P是相联系的。但是水平数相同的正交表其列数和行数也不相同。由此可见正交表的行数K与列数J也是相联系的。因此可以断言，凡是水平数和列数满足实验要求的正交表，其行数K一定满足要求。