指数平滑法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第718页（2184字）

指数平滑法是移动平均法的改进。其基本思路是：在预测研究中越近期的数据越应受到重视，时间序列数据中各数据的重要程度由近及远呈指数规律递减，故对时间序列数据的平滑处理应采用加权平均的方法。

1．一次指数平滑值的计算

假设时间序列数据是一个无穷序列：y_t，y_t－1，y_t－2，…，其加权平均值为

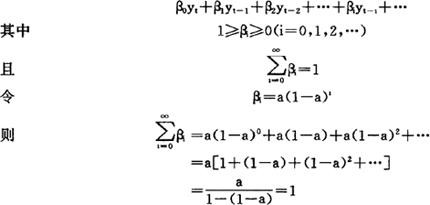
用β_i=a(1－a)¹(i=0，1，2，…)对时间序列数据加权，设加权平均值为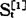，则有

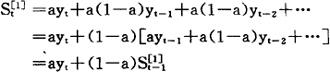
实际上，时间序列数据是有限的，一般情况下，∑β_i＜1，但只要这个时间序列足够长，上式可以作为有限时间序列数据加权平均值的一种近似。这个加权平均值就是我们所要求的一次指数平滑值。所以一次指数平滑值的计算公式为：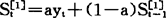

式中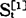——第t周期的一次指数平滑值；

y_t——预测对象第t周期的实际数据；

a——指数平滑系数。

a实际上是新旧数据权重的一个分配比例，a值越大，则新数据在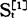中的权重越大。a取值的大小是影响预测效果的重要因素，一般要根据实际时间序列数据的特点和经验确定。如果时间序列数据的长期趋势比较稳定，应取较小的a值(如0．05～0．20)。如果时间序列数据具有迅速明显的变动倾向，则应取较大的a值(如0．3～0．7)。

上式是一个递推公式，计算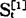时，要先知道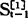，计算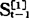时，要先知道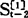，如此递推下去，计算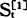时就需要有一个初始值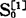。当实际数据比较多时，初始值对预测结果的影响不会很大，可以以第一个数据y₁作为初始值，如果实际数据较少(如20个以内)，初始值的影响就比较大，一般取前几个周期的数据平均值作为初始值。

如果实际时间序列数据的变动主要是随机变动而没有明显的周期变动和增长或下降趋势，我们可以直接用最近一个周期的一次指数平滑值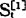。作为下一周期的预测值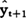。如果求得的一次指数平滑值时间序列数据有明显的线性增长或下降趋势，与移动平均法相类似，由于一次指数平滑值序列相对于实际数据序列存在着滞后偏差，必须在求二次指数平滑值的基础上建立预测模型。

2．二次指数平滑值的计算与线性预测模型的建立

二次指数平滑是对一次指数平滑值序列再作一次指数平滑。二次指数平滑值的计算公式为：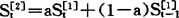

式中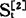——第t周期的二次指数平滑值。

求二次指数平滑值也要先确定初始值，通常直接取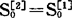，也可以取前几个一次指数平滑值的平均值作二次指数平滑的初始值。

在二次指数平滑处理的基础上可建立线性预测模型

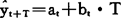
截距a_t与斜率b_t的计算公式分别为：

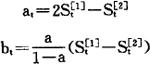
二次指数平滑预测模型仅适用于预测对象的变动趋势呈线性的情况。如果预测对象的变动趋势是非线性的，则应在求三次指数平滑值的基础上建立非线性预测模型。

3．三次指数平滑值的计算与非线性预测模型的建立

三次指数平滑是对二次指数平滑值序列再作一次指数平滑。三次指数平滑值的计算公式为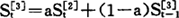

式中】——第t周期的三次指数平滑值。

三次指数平滑的初始值可以直接取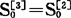，也可以取前几个二次指数平滑值的平均值。

在三次指数平滑处理的基础上可建立如下非线性预测模型：

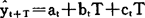
模型系数a₁、b_t、c_t的计算公式为

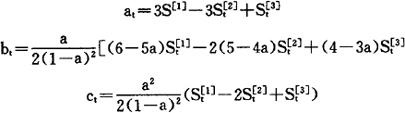
若实际时间序列数据的变动趋势呈线性，

则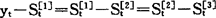代入上述模型系数计算公式，可得c_t=0，a_t与b_t的计算公式简化后与线性预测模型中相同。由此可知，线性预测模型实际上是非线性预测模型的一种特殊形式。

平滑法(包括移动平均法和指数平滑法)适用于寻找实际数据序列的长期变动趋势，对数据序列的转折点缺乏鉴别能力。如果遇到数据序列出现转折点的情况，要靠预测者根据外部影响因素的分析判断对预测值进行修正。