几个重要的基本定律

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第289页（4610字）

1．高斯定律

在真空中的任何静电场中，通过任一闭合曲面的电通量等于这闭合曲面所包围的电荷的代数和的ε₀分之一。其数学表达式为

式中Φ_e为电通量，E和E_n为电场强度及其在法线方向上的分量，dS为面积元，θ为dS的法线n与该处的电场强度E的夹角，q为电荷，ε₀为真空中的介电常数。

2．磁场中的高斯定律

在磁场中，通过任何闭合曲面的磁通量一定等于零。这是由于自然界中没有发现单独存在的磁极的结果。其数学表达式为

式中B和B_n为磁感应强度及其在法线方向上的分量，dS为面积元，θ为dS的法线n与该处的磁感应强度B的夹角。

3．线性电路的欧姆定律

当导体的温度不变时，通过导体的电流与导体两端的电压成正比，与导体的电阻成反比。用公式表示为i=u／r。

4．焦尔－楞次定律

是说明电能可转换为热能的定律

Q=I²Rt (6．2－3)

式中Q为热量，I²Rt为电能，即在时间t内电流I通过一段电阻为R的导体时所消耗的电源的能量。

5．基尔霍夫电流定律(又称基尔霍夫第一定律)

对于任一集中参数电路中的任一节点，在任一时刻，流出该节点的所有支路电流的代数和等于零。其数学表示式为

∑i=0_。 (6．2－4)

6．基尔霍夫电压定律(又称基尔霍夫第二定律)

对于任一集中参数电路中的任一回路，在任一时刻，沿着该回路的所有支路电压的代数和等于零。其数学表示式为

∑U=0 (6．2－5)

7．毕奥－萨伐－拉普拉斯定律

电流元Idl在空间P点产生的磁感应强度为dB，dB的大小为

dB=μ₀Idlsinα／4πr² (6．2－6)

式中的r是从电流元所在点到P点的距离(相应的矢径为r)，α为Idl与r之间小于180°的夹角。dB的方向是垂直于Idl与r组成的平面，指向为由Idl经α角转向r时右螺旋前进的方向。

8．安培环路定律

在磁场中，沿任何闭合曲线的B矢量的线积分(也称B矢量的环流)，等于真空的磁导率μ₀乘以包围在这闭合曲线内各电流的代数和。其数学表达式为：

9．安培定律

电流元在磁场中所受的力，即安培力为

dF=Idl×B (6．2－8)

式中Idl为电流元，B为磁感应强度矢量。

10．磁路的欧姆定律(磁路定律)

以一截面积为S、长为l、磁导率为μ的铁环上绕以紧密的N匝线圈为例，设线圈中通过的电流为I，根据安培环路定律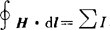，应用到环中任一磁感应线，得到Hl=NI，通过任一截面的磁通量为Φ=BS=μHS，因此Φ=NI／(l／μS)。这个公式与简单回路的欧姆定律I=E／R=E／(l／γS)相比形式相似，如果称NI为磁通势εm，而称l／μS为磁阻R_m(其单位为每亨利)，则磁通与电流相当，可得Φ=ε_m／R_m。磁阻的倒数1／R_m=G_m称为磁导，单位为亨利。

11．楞次定律

闭合回路中产生的感生电流具有确定的方向，它总是使感生电流所产生的通过回路面积的磁通量，去补偿或者反抗引起感生电流的磁通量的变化。

12．法拉第电磁感应定律

通过回路所包围的面积的磁通量发生变化时，回路中产生的感生电动势E_i与磁通量对时间的变化率成正比。在采用国际单位制时，此定律可表示为

E_j=－dΦ／dt (6．2－10)

式中的负号反映了感生电动势的方向，是楞次定律的数学表示。

13．全电流定律

在磁场中沿任一闭合回路H的线积分，在数值上等于该闭合回路内传导电流和位移电流的代数和，即

式中D／t=δ_d称为位移电流密度，I_d(=dΦ_D／dt)称为位移电流(电场中某点的位移电流密度等于该点电位移的时间变化率，通过电场中的某截面的位移电流等于通过该截面的电位移通量的时间变化率)。

14．磁路的基尔霍夫第一定律

在磁路的分支处所联接着的各个磁支路中磁通的代数和应恒等于零，即

∑Φ=0 (6．2－12)

与电路相似，可把分支处称为节点，而联接在节点间的部分磁路称为支路。

15．磁路的基尔霍夫第二定律

磁路中沿任意闭合回路磁压的代数和等于沿该回路磁势的代数和：

∑Hl=∑ωI (6．2－13)

根据全电流定律，当积分的磁回路的各段中，同一段内的截面积相同、材料也相同时，则各点上的磁场强度也相同，如果磁路中各点的磁场方向与各段长度的方向一致，则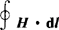可用各段磁场强度与长度的乘积代数和去代替。每一项Hl可看成是磁路中每一段上的磁压或磁位差，有时以U_M和φ_M来表示。式(6．2－13)中的ωI是该回路所链各磁化线圈的电流与匝数相乘的代数和。ωI又可称为磁势(或磁化力)，单位为安匝。

【参考文献】：

［1］国家技术监督局发布，GB3100～3102－93量和单位国家标准，中国标准出版社，1994年12月。

［2］王江主编，现代计量测试技术(第18章电磁计量技术)，中国计量出版社，1990年12月。

［3］程守洙、江之永主编，普通物理学第二册，人民教育出版社，1979年2月。

［4］俞大光编，电工基础，人民教育出版社，1958年9月。

［5］Г．И．阿塔别柯夫，线性电路理论，人民教育出版社，1963年12月。

［6］C．A．狄苏尔、葛守仁，电路基本理论，人民教育出版社，1979年1月。

［7］乔蔚川、刘瑞珉、沈平子，The Absolute Measurement of the Ampere by Means of NMR，IEEE Trans．Instrum．Meas．，vol．IM－29，No．4，Dec．，1980．

［9］张钟华等，NIM用计算电容测定的量子化霍尔电阻的SI值(英文)，计量学报，第16卷，第1期，1995年1月。

［10］刘瑞珉、刘恒基、金惕若等，NIM对γ′_p及2e／h的SI值的最新测定结果(英文)，计量学报，Vol．16，No．3，1995年7月。

［11］B．P．Kibble。I．A．Robinson and J．H．Belliss，A Realization of the SI Watt by the NPL MovingCoil Balance，CCE Documents 88－16，1988．

［12］P．T．Olsen。R．E．Elmquist，E．R．Williams，G．R．Jones and V．E．Bower，A Measurement of the NBS Electrical Watt in SI Units，CCE Documents 88－37，1988．

［13］Report of the 18th Meeting of CCE，1988．

［14］B．P．Kibble，I．A．Robinson and J．H．Belliss，The New NPL Moving Coil Balance-A Progress Report，CCE Documents 92－61，1992．

［15］唐统一、张钟华、张叔涵主编，近代电磁测量，中国计量出版社，1992年8月。

［16］袁楠、沈平子编，电磁量的单位制和单位的复现与传递，机械工业出版社，1986年4月。

［17］阮永顺、迈淑琴、王晓超编着，交流电桥检定与测试技术，中国计量出版社，1991年5月。

［18］唐佐梁、梁德正等，电能计量手册，河南科学技术出版社，1990年12月。

［19］K．J．Lentner．A Current Comparator System to Establish the Unite of Electrical Energy at 60 Hz，IEEE Trans．Instr．Meas．Vol．23，No．4，p．334－336，Dec．，1974．

［20］ю．B．阿法拉谢耶夫等着［苏］，张伦译，磁场参数测量器具，科学出版社，1983。

［21］p．Φ．阿克纳叶夫、Л．И．留必莫夫、A．M．巴纳休克－米罗维齐着，李绍贵，王登安译，电磁量计量器具的检定，中国计量出版社，1992年5月。