电流单位安培的定义及其复现
出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第308页（10363字）
1．基本单位安培的定义
在电磁学领域中，电流的单位安培(A)是国际单位制七个基本单位之一。
电流的物理概念是单位时间内通过导体横截面的电量，即I=Q／t。如在1s内通过导本横截面的电量为1库仑(C)，导体中的电流即为1A。我们知道一个电子电荷约等于1．6×10－19C，如果能测出1s内通过导体某一横截面的电子数，就可复现安培单位。实际上，利用目前的技术还很难实现。
作为计量单位，其定义必须考虑到能够实际复现，因此在近一百年中对安倍的两次不同的定义都与上述的物理概念有区别。如1908年在伦敦举行的电学单位和国际标准国际会议上决定，以电解银的电流来定义“国际安培”(1)。规定：1［国际安培］为：通过在按规定配制的硝酸银水溶液中以每秒0．00111800g的速率电解银时的恒定电流。
目前使用的SI单位制中的安倍是1948年第九届CGPM定义的。安培的新定义为：
“在真空中，截面积可忽略的两根相距1m的无限长平行圆直导线内通以等量恒定电流时，若导线间相互作用力在每米长度上为2×10－7N，则每根导线中的电流为1A。”
这一定义的数学表达式即为：
△F=μ0(I1·I2／2πr)·△l (6．3－1)
式中I1和I2为两导线中分别通以的电流，r为两导线之间的距离，△l为计算作用力时所选定的导线长度，μ0≡4π×10－7N／A2，为真空中的导磁率。这是为了使以新定义的安培为基础的电磁力单位和以米千克秒制为基础的机械力单位相等而引入的一个系数。当r=△l=1m，I1=I2=1A时，△F=2×10－7N。
2．安培的复现和电单位的绝对测量
电流本身没有实物基准，实际上各国都是通过电压(电动势)和电阻的实物基准来复现和保存安培单位。但电压和电阻实物基准所保存的量值均存在着随时间漂移及是否和其定义值(亦称为SI值)相一致的问题。因此，按照定义定期或不定期地复现安培或伏特和欧姆的单位量值就非常必要。在μ0作为精确常数规定之后，安培按其定义通过力学量的基本单位(m、kg、s)来复现，称之为电流的绝对测量。所复现的安培称为SI安培或绝对安培。同样，对电阻、电压和电功率也可进行绝对测量。实际上，通过这些绝对测量所确定的是各国保存的电单位量值ALAB、ΩLAB、VLAB和WLAB与相应的SI值A、Ω、V和W的比值KA、KΩ、Kv和Kw。
一般，一个国家内只在上述四个量中选取两个量进行其绝对测量方法的研究。因为根据欧姆定律和电功率公式I=U／R和P=U·I只要测定了其中的两个量，另两个量即可通过这两个公式求得。
自本世纪20年代至今，各国科学家进行了各种绝对测量方法的研究，有的因其准确度低而被逐渐淘汰，有的至今仍在采用。下面对这些方法予以简单介绍。
(1)电流绝对测量
①电流天平法
本世纪40－60年代，一些主要工业化国家如美、英、苏以及60－70年代民德等都采用电流天平法对电流进行了绝对测量。此方法巧妙地用一个可移动螺线管线圈置于一个固定螺线管线圈中间近似地实现了安培定义中两根无限长且相互平行的直导线的条件，同时用天平称出两线圈通电时的相互作用力。实际上这一装置与安培定义中所要求的条件还不完全相符，不能用(6．3－1)式来计算。实际使用的公式是从麦克斯韦尔电磁理论中选取的两通电回路相互作用的能量公式：W=I1·I2·M，I1、I2分别为两通电回路中的电流，M为两通电回路之间的互感。对此式经过处理可得到：
图6．3－1 电流天平原理图
△F=mg=dW／dX=I1·I2·dM／dX． (6．3－2)
一般都使可动线圈与固定线圈串联，即I1=I1=I，dM／dX可根据线圈的几何尺寸求出。在称出作用力△F后，即可计算出电流的大小。
I=［△F／(dM／dX)］1／2 (6．3－3)
线圈中通过的电流一般为1A，两线圈的相互作用力很小，单是称力这一项就使电流天平的测量不确定度限制在10－6量级，加上线圈几何尺寸及它们之间的相对位置的测量都不可能达到很高的准确度，因此几十年来，电流天平法复现安培的不确定度一直徘徊在百万分之几至十万分之一范围内。目前此方法已被逐渐淘汰。但应该肯定，在电学计量史上电流天平对提高电单位复现准确度曾起过重要作用。
②核磁共振法
核磁共振法是继电流天平之后一种复现安培的新方法。本世纪60年代以来在一些国家中开始研究和应用。它是通过在弱磁场中和在强磁场中分别测定基本物理常数——质子回旋磁比γ′p，利用γ′p(强)与电流成正比、γ′p(弱)与电流成反比的特点，将两者相结合，然后计算得到保存安培与绝对安培之比KA(≡ALAB／A)。
根据核磁共振基本关系式
ωp=γ′p·B (6．3－4)
式中ωp为共振时的质子进动频率，B为质子所在处的磁感应强度值。由上式可见，如果准确知道B值，则可通过测量ωp来测定γ′p值。在强场法和弱场法测量γ′p的实验中，关键都是要建立一个稳定、均匀的磁场，并准确地测量或计算它。同时测量质子(一般均用水中氢原子内的质子)在围绕该磁场进动时在包围它的接收线圈上所感生的电动势的频率。
弱场法又称自由进动法，即质子首先在垂直于主磁场的另一个强磁场中进行极化取向，当该磁场瞬间切断时，质子就开始绕主磁场进动，并在接收线圈上感应出频率为ωp1的随时间衰减的信号。主磁场由以熔融石英为骨架的精密单层螺线管或赫姆霍茨线圈(Helmholtz)产生，线圈直径和螺距用激光干涉仪等仪器精密测定，然后通过计算得到线圈常数C1(即线圈通以单位电流时产生的磁场值)。线圈中的电流I1用补偿法测量，即将该电流在标准电阻(R)上的压降(U)与标准电池电动势相比较，由U／R确定。由此可得到
γ′p(弱)=ωp1／μ0C1I1 (6．3－5)
如用括号｛ ｝表示数值，［ ］表示单位，则上式可表示为
由于主磁场比较弱，一般为0．2～1mT，而地磁场约为0．05mT，因此弱场法中均需要对地磁场进行补偿，且实验需要在无磁实验室内进行。图6．3－2为我国在弱磁场中测定
装置原理图。
图6．3－2 我国弱磁场中测定
装置原理图
强场法亦称共振吸收法。磁场的数量级约为0．5～1T，由磁铁产生。质子样品放在一个与磁场垂直的小激励线圈内，用频率等于ωp2的连续交变场进行激励，使其发生共振。磁场的测量采用天平法，即通过测量置于磁铁极隙中通电矩形线圈与磁场的相互作用力来确定(见图6．3－3)。根据安培定律，长度为dl的导线元通以电流I2，在磁场中所受的力为
图6．3－3 我国强磁场中测定
装置原理图
(6．3－7)
则用精密天平称出的总的垂向力为dF沿矩形线圈回路进行积分的结果，
Fy=mg=I2B0X0 (6．3－8)
g为重力加速度，B0为极隙中心的磁场值，X0称为矩形线圈的有效宽度，可根据线圈的底边宽度、侧边不平行性及场分布系数算出。则
γ′p(强)=ωp2I2X0／mg (6．3－9)
当I2采用与I1相同的实验室保存安培单位ALAB来表示时，上式亦可写为
实际上，(6．3－6)式和(6．3－10)式是相等的，即
由此得
｛γ′p(弱)／γ′p(强)｝1／2=(ALAB／A)≡KA (6．3－11)
同时可得不依赖于ALAB的质子回旋磁比值
γ′p(abs)=｛γ′p(弱)·γ′p(强)｝1／2·(A·s／kg) (6．3－12)
这种绝对测定安培的方法称为间接测量法。我国在中国计量科学研究院建有弱场和强场测定γ′p装置，1977年课题完成时，水平均处于世界第二位。而且我国是第一个在同一实验室内用此法测出KA的国家。当时测量结果的不确定度(1σ)为：γ′p(强)：3．5×10－6，γ′p(弱)：0．80×10－6，KA和γ′p(abs)：1．8×10－6。后经改进，到1988年上述测量定的不确定度为：γ′n(强)：1．55×10－6，γ′p(弱)：7．4×10－7，KA和γ′p(abs)：8．6×10－7。
国际上进行过γ′p(弱)测量的还有美、英、日、原苏联和民德五国，测量准确度最高的是美国NIST，为1．1×10－7(1988年)。苏、英和民德还进行过γ′p(强)的测量。英国NPL的测量准确度最高，为1．0×10－6(1974年)，但这三国后来都中止了这一工作。
(2)电阻绝对测量
电感和电容的电抗ωL和1／ωC都具有电阻的量纲，原理上，它们可以在某一网络或电桥线路中同电阻相比较。因此，电阻的绝对测量都是通过计算电感或计算电容来进行的。
①计算电感法
最早的电阻绝对测量是通过计算电感(包括自感和互感)来实现的。带有电流I的电感器的总能量为
，它可以看成是储存在电感器的磁场的能量
。当采用单位电流时，只要知道了电流密度的分布，利用麦克斯韦方程即可计算出电感量来。但无论是自感还是互感，都需要对线圈尺寸进行精密测量，由于几何尺寸测量误差的影响很难使其不确定度减小到1×10－6以下，而且由于后来计算电容法的出现，计算电感法逐渐被淘汰了。
②计算电容法
1956年澳大利亚科学家兰帕特(D．G．Lampard)和汤姆逊(A．M．Thompson)提出了一个静电学新定理。该定理利用保角变换的黎曼定理证明了一个截面为任意形状的无限长导电柱面，如被四个无限小绝缘间隙α、β、γ和δ分割为四部分时(如图6．3－4所示)，相对两个电极之间单位长度的电容C1和C2，无论电场在柱面内还是柱面外，均满足如下方程
图6．3－4 截面为任意形状的无限长导电柱面
式中C′=(ε0εr／π)ln2为一常数；εr为介质的相对介电常数；ε0为真空介电常数。C1、C2又称为交叉电容。当C1≈C2时，上式可简化成
式中△C=C1－C2。当柱面内部抽真空εr=1，ε0=1／μ0c2是精确的，柱面的轴向长度为l时，则总电容量为：
由(6．3－15)式可见，用此方法建立的计算电容与电极系统的截面形状无关，而只与轴向长度l有关，此长度可以用接近于长度基准的准确度来测量，因此，这种计算电容的不确定度可以小到10－7～10－8量级。
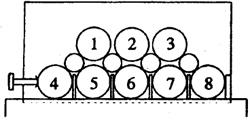
图6．3－5 我国计算电容基准的电极布置图
图6．3－5为我国计算电容基准的电极布置图。2、3(指零棒)、6、7(高压棒)四根棒构成了一个如图6．3－4的工作空间，其它园棒只起支撑作用。2、3两根电极为表面喷镀了金属层的熔融石英管，上面光刻了两条细线作为绝缘气隙。刻线间距就是决定电容值的轴向长度。其它六根电极用不锈钢制成。该计算电容主体的电容量名义值为0．5pF，1978年完成时不确定度为3．5×10－7，后经改进已减小到1×10－7。
由计算电容经电容比对电桥传递到10000pF后，利用平衡方程式为
ωRC=1 (6．3－16)
的直角电桥可传递到交流电阻，再经交直流转换电阻传递到直流电阻，最后通过直流电桥传递到1Ω国家基准组上。1978年我国用此法绝对测定电阻的总不确定度为4．8×10－7。后经改进并已减小为1．8×10－7。
国际上采用此法进行电阻绝对测量的国家还有美、英、法、日、澳大利亚和原苏联。1986－1988年期间，他们测量KΩ的不确定度，前三个国家为(2～6)×10－8，后三个国家为(2～3)×10－7。
(3)电压绝对测量
一般用测量静电引力来绝对测量电压。从静电学理论可知，若两平行金属板之间的电容为C(它是距离的函数)，电位差为U，则能量W为CU2／2。并且在垂直于两板的方向(Z)上存在着相互作用力Fz，该力可表示为：
如果dC／dZ是已知的，则通过测量力就可决定电压。一些国家根据这个原理，研究了两种高精度的电压绝对测量装置，下面予以简单介绍。
①开尔文绝对静电计法这是属于天平装置的类型，故又称为电压天平法。如图6．3－6所示，一对平板电容器，下极板为固定电极，上极板为悬挂在天平一个臂上的可动电极，其周围有保护电极以消除边缘效应的影响。如电极间距离为d，电容为C，加到两极板间的电压为U时，两平行板电极间的静电吸引力Fz为
图6．3－6 开尔文型静电计示意图
式中m为平衡电极间吸引力所加或减的砝码质量。电容C的数值可由计算电容传递，距离d用激光干涉仪测量。目前国际上用此法进行电压绝对测量的有德国PTB和南斯拉夫萨格勒布大学，不确定度分别为2．74×10－7(1992年)和2×10－7(1994年)。
②液体静电计
当上述静电计的下电极用水银代替，同时舍去天平，改用以吸引起的水银质量来计算静电引力，则成为水银静电计。水银放在平的容器中，上部用喷涂导电层的平面玻璃或石英板作成上电极和保护电极。如图6．3－7所示，当外加电压为U时，下电极的水银面会突起一定高度h，如水银密度为ρ，介电常数为ε，电极中心和水银之间的距离为d，由于极间电容C=εS／d(S为上极板面积)，对应上极板部分被吸起的水银质量为m=Shρ，则可得到计算外加电压U的公式：
图6．3－7 水银静电计示意图
U=d·(2gρh／ε)1／2 (6．3－19)
如ε、ρ、g预先知道，d和h又可用激光干涉仪测出，则电压U即可确定。澳大利亚CSIRO／NML1988年用此法绝对测定电压的不确定度为2．7×10－7。
(4)电功率绝对测量
70年代后期，英国NPL的克伯(B．P．Kibble)博士提出了移动线圈的方法，用在电流天平上，将电流天平改造成电功率天平，使电功率的测量准确度一跃提高到1～2×10－7。该方法的原理是：第一步与电流天平的原理及操作完全相同，如图6．3－8所示两载流线圈之间的作用力
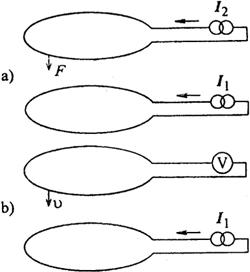
图6．3－8 电功率天平实验原理示意图
当将线圈2开路，并使其相对线圈1运动时(此时线圈1中仍通以电流I1)，在它两端将感应出电动势，
把(6．3－20)式和(6．3－21)式相除，可得
Fzv=I2ε (6．3－22)
式中v=dZ／dt，为线圈移动的速度。式(6．3－22)表明：这装置实现的是机械功率(FZv)和电功率(I2ε)的比较，而且最终表达式中与线圈几何尺寸有关的参数M12消掉了，I1也不必测定，这意味着可以采用数值未知但稳定性好的强磁场源，如磁铁或超导螺管，使FZ比传统电流天平的作用力大2～3个数量级，测量准确度可大大提高。
如将I2表示为以实验室保存的安培单位测得的结果ILAB和安培转换因子KA的乘积，即I2=ILAB·KA，同样可得ε=εLAB·KV，并将它们代入(6．3－22)式，
可得 
(6．3－23)
当由计算电容法测得KΩ后，就可以从KW获得KA和KV：
KA=(KW／KΩ)1／2， KV=(KW／KΩ)1／2 (6．3－24)
由于精确测定瞬时速度和电压是非常困难的，实际上采用的是(6．3－23)式的积分形式，即将式中的感应电动势对时间积分和力对距离积分。
英国NPL用这种方法于1987－88年进行电功率绝对测量的不确定度为1．55×10－7，当和电阻绝对测量结果相结合后，得到的KA和KV的不确定度仅为0．72×10－7。目前仍在继续改进，预计最终可达到1～2×10－8的不确定度。美国NIST也建立了类似的装置，但准确度较英国NPL的低。
3．利用量子基准保存和复现电流的单位安培
1988年9月第18届国际计量大会(CGPM)及第77届国际计量委员会(CIPM)作出决议，决定自1990年1月1日起国际上同时正式启用以约瑟夫森常数KJ－90和冯·克里青常数RK－90的国际公认值为基础的电学计量新基准复现电压单位和电阻单位。这意味着各国原来用实物基准保存和复现电流单位将逐步改变为用电压和电阻量子基准来复现。有关这两个量子基准的原理下面将有介绍，这里应指出的是，由于上述两个常数主要是根据各国电单位绝对测量的结果确定的，分别具有4×10－7和2×10－7的不确定度，因此由这两个量子基准所复现的电流单位量值与真正的SI安倍仍有差别。此外，还应注意，CGPM和CIPM的决议并没有定义新的单位，也没有定义新的物理量。在电磁学领域内，基本单位仍然是安培，安培的定义仍与1948年所规定的一样，没有任何改变。
4．一种有希望的电流量子基准
几年前，科学家发现了一种在极小的隧道结中的电子量子效应，称之为单电子隧道效应。并在此基础上研制了两种称为“栅门”和“电荷泵”的超小型器件，实现了在精确的时间间隔内一个一个地传送电子。1996年美国NIST波尔德分部的实验表明，用这种方法在确定时间内通过数电子来确定电流的不确定度已减小到1．5×10－8量级。目前的主要问题是复现的电流太小，只有pA量级，离实际的计量应用还有不少距离。由于这是一种很有希望的电流量子基准，从事这方面研究的国家已有近十个。
【参考文献】：
［1］国家技术监督局发布，GB3100～3102－93量和单位国家标准，中国标准出版社，1994年12月。
［2］王江主编，现代计量测试技术(第18章电磁计量技术)，中国计量出版社，1990年12月。
［3］程守洙、江之永主编，普通物理学第二册，人民教育出版社，1979年2月。
［4］俞大光编，电工基础，人民教育出版社，1958年9月。
［5］Г．И．阿塔别柯夫，线性电路理论，人民教育出版社，1963年12月。
［6］C．A．狄苏尔、葛守仁，电路基本理论，人民教育出版社，1979年1月。
［7］乔蔚川、刘瑞珉、沈平子，The Absolute Measurement of the Ampere by Means of NMR，IEEE Trans．Instrum．Meas．，vol．IM－29，No．4，Dec．，1980．
［9］张钟华等，NIM用计算电容测定的量子化霍尔电阻的SI值(英文)，计量学报，第16卷，第1期，1995年1月。
［10］刘瑞珉、刘恒基、金惕若等，NIM对γ′p及2e／h的SI值的最新测定结果(英文)，计量学报，Vol．16，No．3，1995年7月。
［11］B．P．Kibble。I．A．Robinson and J．H．Belliss，A Realization of the SI Watt by the NPL MovingCoil Balance，CCE Documents 88－16，1988．
［12］P．T．Olsen。R．E．Elmquist，E．R．Williams，G．R．Jones and V．E．Bower，A Measurement of the NBS Electrical Watt in SI Units，CCE Documents 88－37，1988．
［13］Report of the 18th Meeting of CCE，1988．
［14］B．P．Kibble，I．A．Robinson and J．H．Belliss，The New NPL Moving Coil Balance-A Progress Report，CCE Documents 92－61，1992．
［15］唐统一、张钟华、张叔涵主编，近代电磁测量，中国计量出版社，1992年8月。
［16］袁楠、沈平子编，电磁量的单位制和单位的复现与传递，机械工业出版社，1986年4月。
［17］阮永顺、迈淑琴、王晓超编着，交流电桥检定与测试技术，中国计量出版社，1991年5月。
［18］唐佐梁、梁德正等，电能计量手册，河南科学技术出版社，1990年12月。
［19］K．J．Lentner．A Current Comparator System to Establish the Unite of Electrical Energy at 60 Hz，IEEE Trans．Instr．Meas．Vol．23，No．4，p．334－336，Dec．，1974．
［20］ю．B．阿法拉谢耶夫等着［苏］，张伦译，磁场参数测量器具，科学出版社，1983。
［21］p．Φ．阿克纳叶夫、Л．И．留必莫夫、A．M．巴纳休克－米罗维齐着，李绍贵，王登安译，电磁量计量器具的检定，中国计量出版社，1992年5月。