量本利分析决策法

出处：按学科分类—经济 南京大学出版社《新编经济师实用手册工业企业分册》第157页（2343字）

这是运用“方法篇”(八)中的各种模型来进行决策的方法。这里讨论几种常见的决策问题。

1．经营安全目标决策

假设某企业产品的单价W=50元，各项成本费用如表所列。该企业初定下期的目标利润P为2．2万元，现用量本利分析来判断该目标的安全程度，并确定经营安全的目标值P目。

此问题的决策，需确定计算经营安全率B的有关数据，如果B值表明P是安全的，初定目标可行；若不安全，则需调整P至安全的数值P_目。通常可分五步分析来进行：

(1)分类统计量本利分析所需成本值。根据成本表，可得F=6．6万元，C_v=28元／台。

(2)计算盈亏平衡的产量X_。或销售额S_o，由X_o=F／(w－C_v)和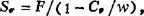代入已知的M、F、C_v就可直接计算得X_o=3000元、S_o=15万元。

(3)计算P=2．2万元时的产量X或销售额S。根据产量模型或销售额模型(即式2－38或式2－41)，也可直接代入已知参量计算得到X=4000元，S=20万元。

(4)计算经营安全率B。根据第2和第3步计算得到的X_o和X，或S_o和S_，就可直接利用经营安全性分析模型(即式2－44或式2－45)得到B=0．25。

从经营安全程度表中可见，当B=0．25时，经营处于不太安全的状况。为保证安全，有必要调整目标，即使B＞0．3。

(5)假设B目=0．3。再利用经营安全分析模型，此时的未知数是产量X_目，或销售收入S_目。将模型式移项变换就得X_目=X。／(1－B)或S_目=S_o／(1－B)，代入已知数得X_目=4286台，S_目=21．43万元。

将X_目和S_目代入量本利基本模型就可得此时的P_目=2．83万元。

决策的结论：经营安全的目标应为X＞4286台或S＞21．43万元，以保证P＞2．83万元。

上述决策没考虑使盈亏平衡点左移的措施，若产量无法扩大到4286台，就需用这类措施来提高经营安全性，如降低成本费用等。

2．设备更新方案决策

假设某种设备需更新，有两个方案供选择，方案Ⅰ的投资少于方案Ⅱ，但方案Ⅱ的可变成本比方案Ⅰ少，此时应如何决策?

此问题中，两个方案的成本有以下特点：F₂＞F₁，C_v2＜C_v1，所以，它们的总成本C₁和C₂随产量的变化而不同，如图6－3所示。图中的两条成本线与S线之间有三个交点，它们对应的X_o1是方案Ⅰ的盈亏平衡产量；X_o2是方案Ⅱ的盈亏平衡产量，而X_c则是两个方案优劣相当的产量。这种量本利分析图，为决策者提供了直观的三种决策依据：

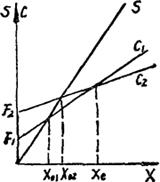
图6－3

(1)当预测的产品产量X＜X_o1时，两个方案都得不偿失，更新会造成亏损，故不应更新；

(2)当X_o1＜X＜X_c时，方案Ⅰ优于方案Ⅱ；

(3)当X＞X_c时，方案Ⅱ优于方案Ⅰ。

这种方法还用于零配件是自制还是购买的决策，此时自制方案需增加生产的固定费用，但自制的C_v将大于购买的单价W_。这样图6－3中的C₁线相当于购买方案的总成本，C₂线相当于自制方案的总成本，则当需要量X＜X_c时，购买方案为优；当X＞X_c时，自制方案为优。

3．产品价格决策

假设某产品的销售量X一定，F和C_v已知，如何定价(即求W值)。

此问题有两种情况的决策：

(1)确定盈亏平衡的价格。此时将预测的销售量X作为已知的盈亏平衡产量，用盈亏平衡的产量模型求出价格W_o，(W_o=(F+C_v·X)／X)，则销售价W＞W_o即可。

(2)确定能够实现一定利润P的价格。此时只有当生产成本在市场上有优势，决策价格能被用户接受的情况下适用。确定时直接用产量模型，将W作未知数，代入P、X、F、C_v即可求出。

若预定的P值使价格太高，则应反过来将W调整到适度值，再相应地调整可实现的利润。

4．产品组合生产方案决策

此类问题是利用量本利分析的边际贡献模型，根据各品种的临界收益M_i和临界收益率mj值，求出产品组合生产的累计值∑S_j和∑M_j，从而得到∑P_j(=∑M_i－F)。再根据市场销售情况，调整产品组合生产方案，以实现∑P最大的组合生产。案例分析见“决策篇”(三)。