逻辑代数读图法

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册下》第2814页（3195字）

继电控制常用的电器元件，一般只有两个工作状态，因而可采用逻辑代数予以描述、分析。在逻辑代数中，把两个对立的物理状态的量(如线圈的得电或失电，行程开关的受压或未受压，触点的吸合或释放等)，称为逻辑变量。在继电控制电路中，通常把表征触点状态的逻辑变量称为输入逻辑变量，把表征受控元件线圈的逻辑变量称为输出逻辑变量。输入、输出变量的相互关系，就是函数关系，故称输出变量是各输入变量的逻辑函数。为了建立触点组合和逻辑变量运算，电路状态与逻辑函数式之间的对应关系一般作如下规定：

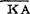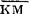
①用KA_图、KM_图……分别表示继电器、接触器的线圈；用KA、KM、SQ……分别表示继电器、接触器、行程开关的动合(常开)触点；用、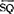……分别表示继电器、接触器、行程开关的动断(常闭)触点。

②电路中开关元件受激状态(如继电器线圈得电；行程开关受压状态)为“1”状态；开关元件的原始状态(如继电器线圈失电，行程开关未受压状态)为“0”状态。触点的闭合状态为“1”状态，触点的断开状态为“0”状态。由此，以下各式的意义是：KM_图=1为接触器线圈处于得电状态；KM_图=0为接触器线圈处于失电状态；KM=1为接触器动合(常开)触点处于受激吸合状态；KM=0为接触器动合(常开)触点处于原始断开状态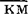；=1为接触器动断(常闭)触点处于原始闭合状态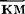；=0为接触器动断(常闭)触点处于受激断开状态；SB=0为按钮动合触点处于原始断开状态；SB=1为按钮动合触点处于受压闭合状态；SB=0为按钮动断触点处于受压断开状态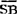；=i为按钮动断触点处于原始闭合状态。

③电路中电器元件触点的串联以逻辑乘(“与”或者“●”)的关系表示：并联以逻辑加(“或”或者“+”)的关系表示。

从上述规定看出，开关元件本身状态的“1”、“0”取值和它的动合触点的“1”、“0”取值一致，而和其动断触点的“1”、“0”取值相反。

为了便于处理逻辑问题，逻辑函数有多种表示方法，如逻辑表达式、真值表、卡诺图、逻辑图和继电控制线路图。在继电控制线路(不涉及桥形电路)中，是用触点的串联、并联、串并联的复合结构进行逻辑运算的，并能用逻辑函数式来描述。反之，逻辑函数也可用继电控制线路图表示。也就是说，逻辑代数中的一些基本公式和定律，是与相应的继电控制线路相对应的，一方面能用继电控制线路的逻辑功能进一步验证这些公式、定律，另一方面可用这些基本公式、定律为继电控制线路服务。例如，利用反演定律可将“与非”变成相应的“或”，而将“或非”变成相应的“与”。这样，继电控制线路的“与非”和“或非”的运算，就可不用繁杂线路，而使用相应的并联或串联线路即可。

继电控制线路通常为串接电路，也就是将电器元件线圈串接在由触点构成的两端网络，然后与电源相接。按照一般规定，以电器元件线圈为函数，其函数式的写法是：从电源一端开始，与此线圈相连接的动合触点写原变量，动断触点写反变量，串联的触点为“与”，并联的触点为“或”，直至写到电源的另一端。用这种方法，就可写出每个线圈的“与或”形式的逻辑表达式。再利用“1”和“0”的规定，就可知线圈在什么条件下得电，什么条件下失电。例如，图8．4－36中的KA1_图的逻辑式可写为：

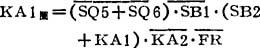
画串接电路的方法是，先将逻辑函数表达式变换成“与或”形式，再由电源的一端开始画，原变量为动合触点，反变量为动断触点，“●”为串联，“十”为并联，直至画到与线圈相串接，再与电源的另一端相连接。注意，各个逻辑函数表达式中相同的逻辑式可共用一个线路。

用逻辑代数阅读继电控制线路图的方法，简称逻代法。逻代法读图的第一步，是写出继电控制线路图中各控制元件、执行元件线圈的逻辑表达式。第二步，是记住初始状态时各逻辑变量的状态，然后操纵主令电器，如按钮或开关等。当发出主令控制信号后，观察逻辑函数式为“1”以及由于相互作用而使逻辑函数式为“1”者，再综合到执行元件有何动作或运动，及其驱动被控对象的运动情况。若有自动电器，还应考虑自动电器动作完毕的影响和动作。如果有自动循环，则应观察由于执行元件驱动机械运动而使哪个检测信号元件的状态发生变化，又使哪个逻辑函数式为“1”……，然后再综合到执行元件有何运动，以及由它驱动的被控对象有何运动……，一直查到底。这样，就可全面地看到各个逻辑及其相互制约的关系。这种读图方法，只要控制电器线圈逻辑式写得正确，各控制元件之间的联系、制约关系就能一目了然，其控制功能也不会看错或遗漏；能做到简明扼要地叙述继电控制线路图的工作原理。

例8．4－3 图8．4－36中主轴和进给电动机的正反向点动和停车反接制动的控制，采用逻代法进行读图。

首先，写出低速时的有关逻辑函数的逻辑式：

关于主轴及进给电动机正反向点动控制，假设主轴和进给已变速，并且高低速转换手柄为低速档，由表8．4－6和8．4－7可知：

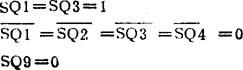
因是点动操作，故不按SB2和SB3，则SB2=SB3=0，接通电源开关QS，从式(8．4－1)～(8．4－6)可以看出：

由于接触器KM1控制M1正转，故触点KV－2=0。同理，KM2控制反转，速度继电器的KV－1=0。则

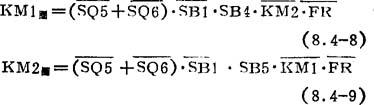
正向点动时，按SB4，由式(8．4－7)～(8．4－9)可知其无自锁，则KM1_图=1；KM2_图=0；KM4_图=1。从主电路看，双速电动机M1正转、定子绕组△形接法、串入电阻R，降压起动，低速运行。若松开按钮SB4，则SB4=0，KM1_图和KM4_图相继为0，即M1停止运转，没有接入反接制动。

反向点动控制，按SB5，则KM1_图=0；KM2_图=1；KM4_图=1。M1反转、降压起动，低速运行。松开SB5，KM2_图、KM4_图相继为0，M1电机停止运转。

关于主轴和进给电动机停车及反接制动，除以上的假设外，再假设为正转运行。从式(8．4－1)～(8．4－6)可知：

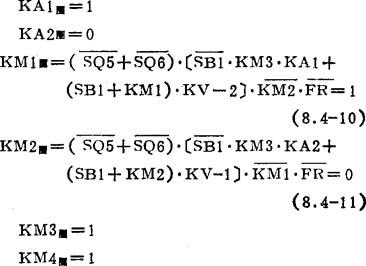
M1正转低速运行。停车时，揿按SB1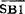，=0，SB1=1时，使KA1_图=KM3_图=0，相继使KM1_图=0，KM2_图=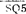+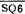)·(SB1+KM2)·KV－1·KM1·FR=1，KM4_图仍为1；当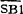=1，SB1=0时，上述状态不变，M1电机接入反相序电源、串入电阻，进入反接制动。当惯性转速为零时，KV－1=0，KM2_图=0，又相继使KM4_图=0，此时切除M1反相序电源，反接制动结束。可以看出，M1反转低速运行的停车反接制动过程，类同正转低速运行的停车反接制动过程，其主要不同点是KM1_图和KV－2起作用。