空间RSSR四杆机构

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1945页（3312字）

图5．5-11所示为含有首末两个转动副和两个中间球面副的空间RSSR四杆机构。杆4为机架。由于主动杆1通常为曲柄，而从动杆3多数为摇杆，故也常称其为空间曲柄摇杆机构。由于连杆2具有绕本身轴线转动的局部自由度，运动不确定而不便利用，所以对该机构进行运动的分析，主要是求出从动杆转角随主动杆转角而变化的运动关系。这里采用比较简便的“拆杆法”，即设想将连杆2拆离进行分析。

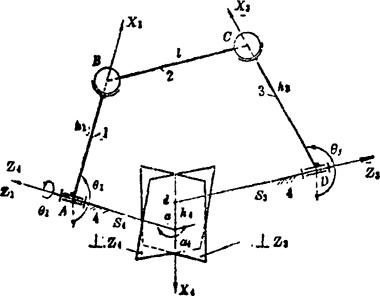
图5．5-11 空间RSSR四杆机构

用矩阵坐标变换法研究机构时，为了把机构的运动转化为坐标系间的变换，在需要分析运动的杆件上均固结有各自的坐标系。图中，与机架4、主动杆1及从动杆3分别固结有坐标系a－X₄(Y₄)Z₄、A－X₁(Y₁)Z₁、及D－X₃(Y₃)Z₃。拆离的连杆2，则不设置坐标系。为了图面清晰，图中只标出各坐标系中的X轴和Z轴。实际上，只要确定了X轴和Z轴，按右手法则，Y轴也随即确定下来。

坐标系的选择原则，主要是应能满足进行坐标变换的要求。通常是先选定各个Z轴，然后沿每两个相邻Z轴的最短距离线(即公垂线)标出各个X轴。图中，Z₁轴和Z₃轴分别选取沿主动杆1和从动杆3的转动轴线，而与机架4相固结的Z₄轴则取其与Z₁轴相重合(也可取得与Z₃轴相重合)；X₁轴与过球面副中心B所作Z₁轴的垂线相重合；X₃轴与过球面副中心C所作Z₃轴的垂线相重合；X₄轴则选在Z₃和Z₄两轴线的公垂线方向，确定各杆的固定坐标系后，可得机构的几何常量参数和运动变量参数如下：

h₁=AB——主动杆长度，由A至B的距离，与X₁轴正方向一致时取为正值；

l=BC——连杆长度；

h₃=DC——从动杆长度，由D至C的距离，与X3轴正方向一致时取为正值；

h₄=da——机架长度，由d至a的距离，与X₄轴正方向一致时取为正值；

s₃=dD——确定从动杆轴向位置由d至D的距离，与Z₃轴正方向一致时取为正值；

s₄=aA——确定主动杆轴向位置由a至A的距离，与Z₄轴正方向一致时取为正值；

a₄——机架角度，对着X₄轴观察，绕X₄轴，由Z₃轴逆时针方向量至Z₄轴为正；

θ₁——主动杆的转角，即输入角，对着Z₄轴观察，绕Z₄轴，由X₄轴逆时针方向量至X₁轴为正；

θ₃——从动杆的转角，即输出角，对着Z₃轴观察，绕Z₃轴，由X₄轴逆时针方向量至x₃轴为正。

采用拆杆法，设想将连杆2拆离时，其余的构件组成开式运动链。从动杆3也和主动杆1-样，能对机架4自由转动。应用不共原点的坐标变换关系，可以写出B、C两点在参考坐标系a－X₄(Y₄)Z₄中的时变坐标。

就坐标系a-X₄(Y₄)Z₄和A-X₁(Y₁)Z₁而言，由于B点在A－X₁(Y₁)Z₁中的坐标为〔h₁，0，0〕^T，而坐标系的变换路线为

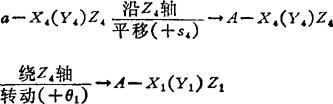
故可写出矩阵变换坐标关系式为

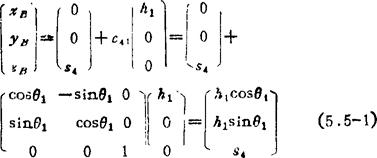
就坐标系a－X₄(Y₄)Z₄和D-X₃(Y₃)Z₃而言，由于C点在D-X₃(Y₃)Z₃中的坐标为〔h₃，0，0〕T，而坐标系的变换路线为

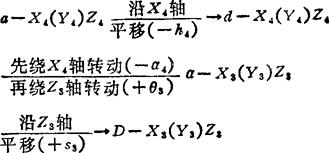
故可写出矩阵变换坐标关系式为

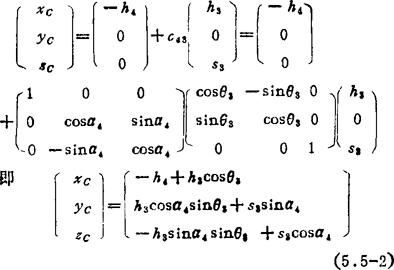
从拆离的连杆2考虑，不管连杆如何运动，B、C两点间的距离始终保持定长l。在实际机构中，由于主动杆的B点和从动杆的C点都是通过球副用定长的连杆相连的，机构运动时，B、C两点的时变坐标要受到连杆定长的约束。因此，设想拆离连杆2后，机构运动仍应保持下列几何等同关系式：

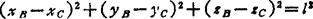
将式(5．5-1)及(5．5-2)代入并展开整理，可得机构的输出输入方程式：

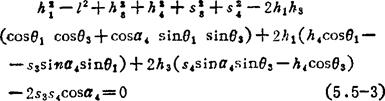
为了求解输出角θ₂，可将上式写成如下形式的三角方程式

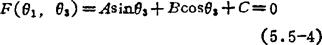
式中系数A、F、C与机构的常量参数和输入角有如下关系：

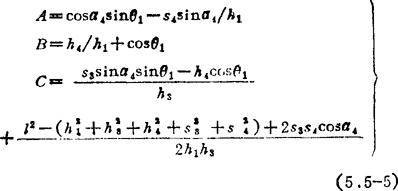
为了便于用代数法求解θ₃，再令x=tg(θ₃／2)，于是有sinθ₃=2x／(1+x²)，cosθ₃=(1－x²)／(1+x²)，从而式(5．5-4)可化成下列二次方程式：

(B-C)x²－2Ax(B+C)=0

解出x得

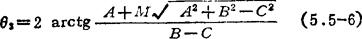
式中 标识符M=±1，表示给定θ₁时，θ₃可有两个值(这与用图解法求解时可有两个交点相当)。M=十1或－1，应该根据所给机构的装配方案或从动杆运动连续性选定。一般来说，符号M只需一次选定，在以后的连续计算中不改变。

将式(5．5-4)对时间求导一次，并令dθ₁／dt=ω₁和dθ₃／dt=ω₃，经过整理后可得：

如果从动杆3有瞬时速度为零的极限位置存在，则在上式中令ω₃=0，可得从动杆3处于极限位置时输入角和输出角之间的关系式为，

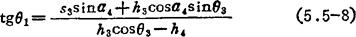
将式(5．5-7)对时间求导一次，并考虑到主动杆作等速转动，即ε₁=dω₁／dt=0，可得从动杆的角加速度公式为：

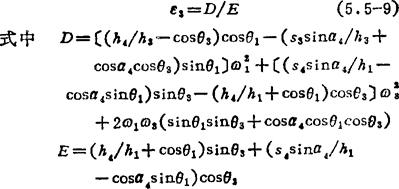
例5．5-1 在图5．5-12所示空间RSSR机构中，主动杆AB、连杆BC和从动杆CD的长度分别为250mm、1100mm和550mm。主动杆和从动杆的转轴垂直交错，它们的转动平面和两轴之间的相互尺寸为l₁=l₂=700mm及l₃=350mm。设主动杆AB以等角速度ω₁=100rad／s转动时，要求对该机构从动摇杆CD作运动分析。

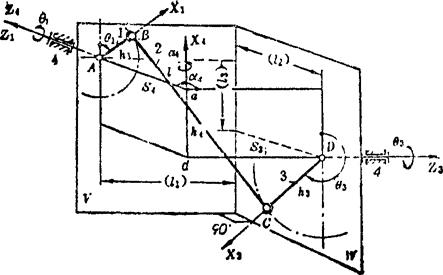
图5．5-12 空间RSSR机构

解：在图示RSSR机构中标注坐标系，并对应图5．5-11比较可知：h₁=250mm。l₁=1100mm，h₃=550mm，h₄=350mm，S3=S₄=700mm，a₄=90°，ω₁=100rad／s。将以上已知结构参数和运动参数分别代入式(5．5-5)、(5．5-6)、(5．5-7)、(5．5-9)，取M=－1，经过编程计算，可解得从动摇杆CD的角位移θ₃、角速度ω₃、及角加速度ε₃。各运动参数对应主动曲柄AB不同位置时的具体数值见表5．5-1。绘制成的运动曲线如图5．5-13所示。

表5．5-1

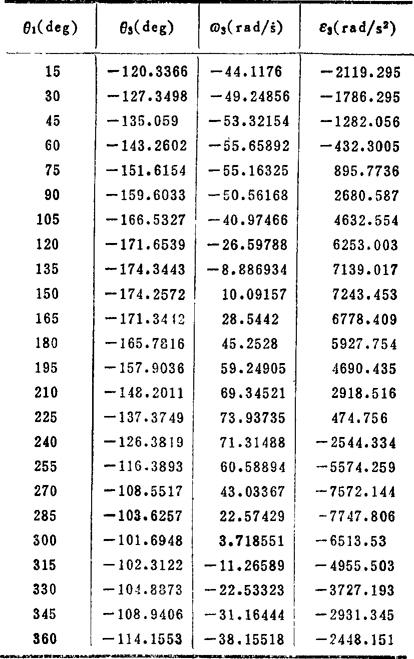
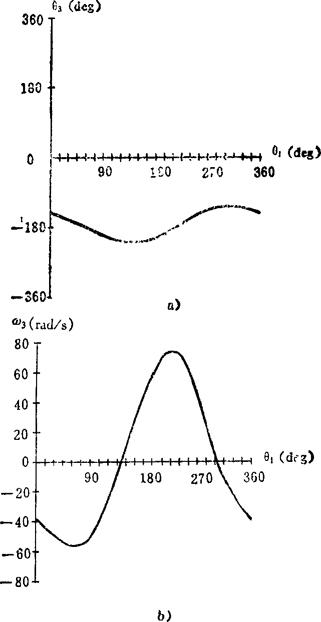
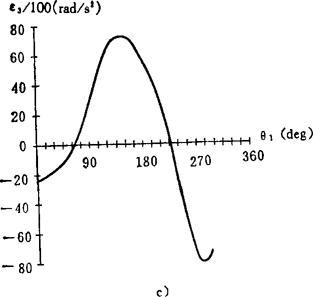
图5．5-13 运动曲线