操作手的运动方程

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2083页（2479字）

用齐次变换矩阵来表示操作手每一杆的位置和方位，其目的是最终求得末端夹持器的位置和方位。图5．13-31所示是PUMA机器人的结构。机器人各杆之间一般用转动关节或移动关节连接。从基座开始对杆编号：基座编为零号，建立固定的基座坐标系；基座与1号杆连接组成的关节编为1号关节。以此类推，末端夹持器的编号为N，它与前面的杆以编号为N的关节连接。第i杆一前一后共有二个关节，其编号为i和i+1。每个关节都有驱动器。驱动器使关节作相对转动或移动，形成末端夹持器的位置和方位的变化。在每个杆上建立一个连杆动坐标系。通常连杆坐标系的原点选在关节的轴线上，而z轴就是该关节的转动轴或移动轴。在i+1关节上建立i杆的连杆坐标系x_j，y_j和z_j，它们相互正交并表示坐标轴的单位矢量。坐标系与i杆固结一起运动。如图5．5-32所示，z_j就是i+1关节轴上的单位矢量。以后简称i+1关节上的连杆坐标系为i杆系。

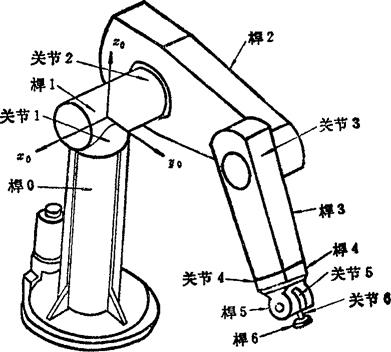
图5．13-31 PUMA机器人的杆和关节

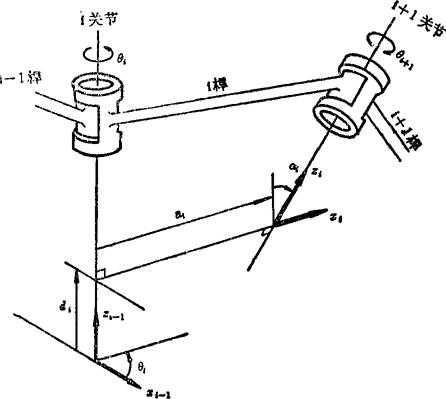
图5．13-32 杆系和杆的几何参数

Denavit和Hartenberg 1955年提出建立杆系的规则(称为D-H表示法)：1．z_j在i+1关节的轴上；2．在i关节轴和i+1关节轴之间作一根公垂线，x_j在公垂线上并且指向公垂线的外延方向，3．y_j垂直x_j和z_j，其方向由右手定则确定。

PUMA机器人有6个杆，因此有6个杆系。基座坐标系编号为零，简称为定系。z。在第一关节轴上，而x₀和y₀的方向是随意的。第六个杆系在末端夹持器上，x₅必须垂直z₅。

按照D-H表示法，一个杆共有4个几何参数θ_j、d_j、a_l和α_j。θ_j是从xj-₁至x_j轴之间的夹角；d₁是i-1杆系原点至x_j轴与z_j-₁轴交点之间的距离；a_j是z_j-₁和z_j轴之间的最短距离；α_j是从z_j-₁轴至zj轴的歪扭角。对于转动关节，d_j、a_j和a_j是杆的几何参数，而且是不变量，θj是关节变量。对于移动关节，θ_j、a_j和a_j是杆的几何参数，而且是不变量，d是关节变量。

相对于i-1杆系，按D-H规则，建立第i杆系的齐次变换矩阵，用来表示i杆系相对i-1杆系的位置和方位。其建立过程是：1．绕i-1杆系的z_j-₁轴转θ_j角，使x_j-1和x_j平行；2．沿z₁-₁轴方向移动d_j，使xj-1和xj重合；3．沿x_j轴方向移动a_j，使原点重合；4．绕i杆系的x_j轴转a_j角，得到i杆系的位置和方位。

上述移动和转动是相对于连杆坐标系(即杆系)进行的，应依次右乘。于是得相邻二杆系的D-H变换矩阵为：

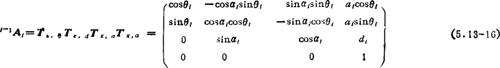
利用(5．13-6)式，上述矩阵的逆为

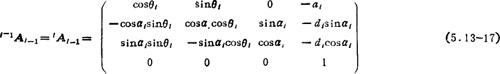
如果i杆上有一点P_j，它在i杆系上的齐次坐标为p_j=〔x_ly_tz_l1〕^T，在i-1杆系上的齐次坐标为p_j-1=〔x_l-1y_l-1z_l-11〕^T，则

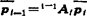(5．13-18)

图5．13-33和5．13-34分别是PUMA和Stanford机器人的杆系和几何参数。

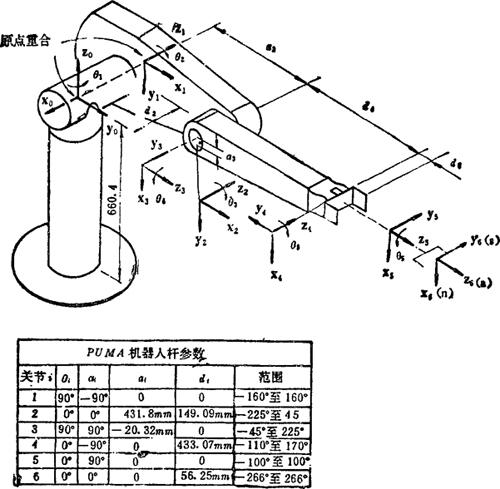
图5．13-33 PUMA机器人的杆系和几何参数

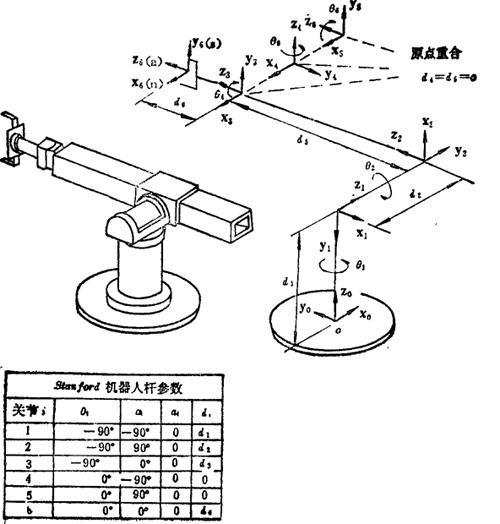
图5．13-34 Stanford机器人的杆系和几何参数

第i杆系在基座坐标系中的位置⁰p_j和方位⁰Dj以齐次变换矩阵⁰A_j表示。它是从基座到i杆系齐次变换矩阵^j－1A_l的链乘积，即

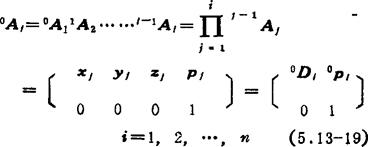
对于PUMA机器人其相邻杆系的齐次变换矩阵为(参看5．13-16式)：

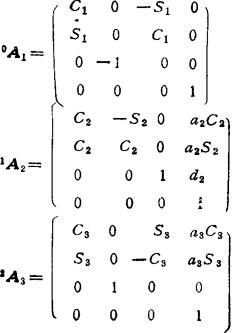
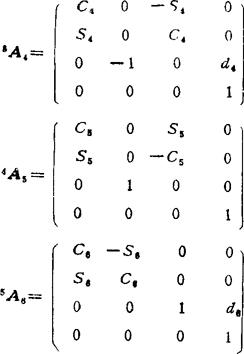
其中，C_j=cosθ_l；S_j=sinθ_j。

操作手运动学的正问题是要求末端装置上的连杆坐标系(第6杆系)在基座坐标系中的位置和方位，即求

T=⁰A₀=⁰A₁¹A₂²A₃³A₄⁴A₅⁵A₆(5．13-20)

式中T称为臂矩阵。末端装置上的连杆坐标系(第6杆系)的坐标原点在夹持中心，其指向由三个单位矢量n、s和a确定，如图5．13-35所示。可以看出

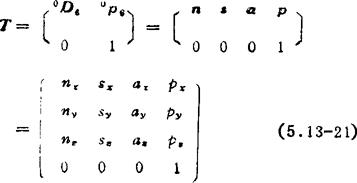
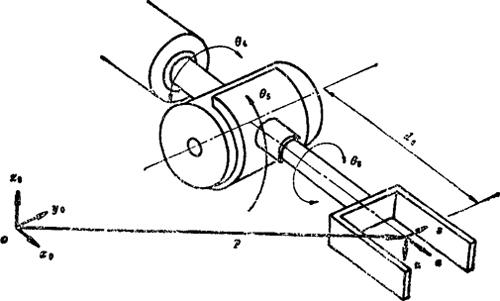
图5．13-35 末端装置上的连杆坐标系

其中，n=夹持器的法向矢量，它垂直手指；8=夹持器的滑动矢量，它在手指开合方向：a=夹持器的接近矢量：p=夹持中心的位置矢量。规定n=。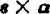

为了减少数值计算的工作量，一般把前三个矩阵相乘，得T₁=⁰A₁¹A₂²A₃(T₁决定夹持器的位置)：把后三个矩阵相乘，得T₂=³A₄⁴A₅⁵A₆(T₂决定夹持器的方位)，最后再由计算机完成T=T₁T₂的数值计算。对于PUMA机器人：

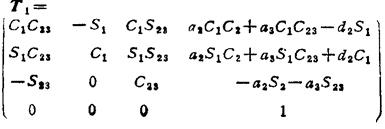
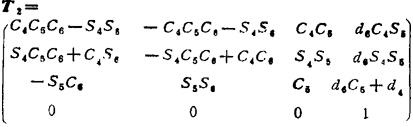
这里C_tj=cos(θ_j+θ_j)；S_jj=sin(θ_j+θ_j)。数值运算中计算机基本没有作与零相乘的空运算，因此节省了机时。