x2—分布

出处：按学科分类—经济 湖北人民出版社《企业管理公式辞典》第36页（432字）

小样本推断中最常用的分布。

英国统计学家卡尔·皮尔逊提出。设x₁，x₂，……，x_n是相互独立，且同服从于标准正态分布的随机变量，则随机变量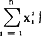服从参数为n(称为自由度)，密度函数为：

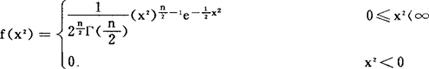
的分布，即称为x²－分布。

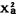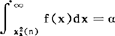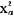其期望值为n，方差为2n。x²－分布上100α百分位点(n)是指满足的点(n)。

对不同的α及n的100α百分位点有x²表可查。该分布与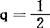，p=n时的Γ分布相同。当n很大时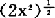近似服从正态分布N(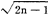，1)。统计中常用的有关x²－分布的理论结论有如下的定理。

定理1：若X为具有方差σ²的正态变量，S²为抽自X的总体，容量为n的随机样本的样本方差，则nS²／σ²服从自由度为n－1的x²－分布。定理2：如果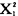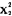，彼此独立且分别服从自由度为v₁、v₂的x^2－分布，则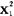+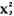服从自由度为v₁+v₂的x²－分布。x²－分布在列联表、方差估计、分布和随机样本参数的假设检验中有着广泛的应用。