数列的表示方法
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第24页(1382字)
从函数的观点看,数列的表示方法有如下三种:
(1)解析法:用通项公式或其他式子表示数列;
(2)列表法:数列可以看作是列表法给出的函数(定义域为正自然数集,或它的有限子集{1,2…n}),自变量省略,只列出函数值;
(3)图象法:数列可以用图形(一群孤立的点)来表示.
利用数列的通项an求数列的最大项或最小项,
若求最大项an,则an满足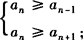 ;若求最小项an则an满足
;若求最小项an则an满足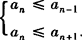 .
.
例1 根据下列数列前n项的值,写出数列的一个通项公式.

解 (1)把数列的前n项写成
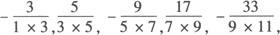
由于数列的各项正、负交替出现,因此每项都有一个因子(—1)n,
又分子构成的规律可记为2n+1,分母为两个连续奇数的积,
∴通项公式为:
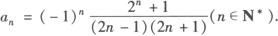
(2)数列9,99,999,…,前几项可以写成10—1,102—1,103—1,…,
∴通项公式为:
an=10n—1(n∈N*).

∴数列的通项公式为
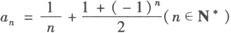
例2 已知下面各数列{an}的前n项和Sn的公式,求{an}的通项公式.
(1)Sn=2n2—3n;
(2)Sn=3n—2.
解 (1)a1=S1=—1.
当n≥2时,an=Sn—Sn1
=(2n2—3n)—[2(n—1)2—3(n—1)]
=4n—5
由于a1也适合此等式,
∴an=4n—5(n∈N*).
(2)n=1时,a1=S1=1.
当n≥2时,an=Sn—Sn—1=2·3n—1.
由于a1不适合此等式,