平面向量的数量积

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第49页（1034字）

1．a与b的夹角：已知两个非零向量a、b，过O点作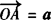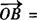，b，则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角．

a与b同向时θ=0°，a与b反向时θ=180°；θ=90°时称a与b垂直，记作a⊥b．特别地，0与任何向量之间无夹角之说．

2．数量积的定义：a与b是两非零向量，它们的夹角为θ，则将|a||b|cosθ叫做a与b的数量积(或内积)，记为a·b，即a·b=|a||b|cosθ．．规定0·a=0(注意与0·a=0的区别)．．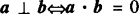

3．a·b的几何意义

(1)一个向量在另一个向量上投影

设θ是a与b的夹角，则|a|cosθ称作a在b的方向上的投影．|b|cosθ称作b在a方向上的投影．

注 投影是一个数而不是向量．故向量数量积的结果是一个数．

(2)a·b的几何意义：a·b等于a的长度与b与a方向上的投影的乘积．

4．a·b的性质

设a·b是两个非零向量，e是单位向量，于是有：

(1)e·a=a·e=|a|cosθ

(2)a⊥b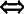a·b=0

(3)当a与b同向时，a·b=|a|·|b|；当a与b反向时，a·b=—|a|·|b|，特别地，a·a=a²=|a|²，或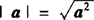

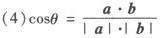
(5)|a·b|≤|a|·|b|

5．a·b的运算律

(1)a·b=b·a

(2)(λa)·b=λ(a·b)=a·(λb)(λ∈R)

(3)(a+b)·c=a·c+b·c