复数的模

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第140页（2693字）

表示复数z=a+bi的向量的长度r叫做复数z=a+bi的模(或绝对值)．记作|z|或|a+bi|．易知|z|=|a+bi|=r=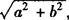，当b=0时，复数a+bi表示实数a．此时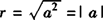，即a在实数意义上的绝对值．

例1 已知i是虚数单位，求1+i¹+i²+i³+…+i²⁰⁰³．

解 利用i²=1．

1+i¹+i²+i³+…+i²⁰⁰³

=(1+i¹+i²+i³)+(i⁴+i⁵+i⁶+i⁷)+…+(i¹⁹⁹⁶+i¹⁹⁹⁷+i¹⁹⁹⁸+i¹⁹⁹⁹)+(i²⁰⁰⁰+i²⁰⁰¹+i²⁰⁰²+i²⁰⁰³)

=(1+i—1—i)+(1+i—1—i)+…+(1+i—1—i)+(1+i—1—i)=0．

例2 m分别为何实数时，复数

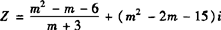是

(1)实数；(2)虚数；(3)纯虚数．

解 利用相关知识，转化为解关于i的方程或不等式问题．

实部为

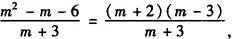
虚部为m²—2m—15=(m+3)(m—5)

(1)要使z是实数，必须

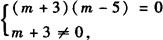
∴m=5时z是实数．

(2)要使z为虚数，必须(m+3)(m—5)≠0，

∴当m≠5且m≠—3时，z为虚数．

(3)要使z为纯虚数，必须

∴当m=—2或m=3时，z为纯虚数

例3 已知关于x、y的方程组

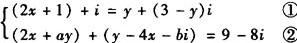
有实根，求a、b的值．其中a、b∈R

解 ∵x、y∈R，据复数相等的充要条件，由方程①式得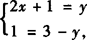

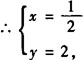
代入方程②，

例4 已知关于t的一元二次方程t²+(2+i)t+2xy+(x—y)i=0，(x、y∈R)

(1)当方程有实根时，求点(x，y)的轨迹方程；

(2)求方程的实根的取值范围．

解 (1)和上例相比，方程中有三个参数t、x、y，由复数相等的充要条件能得到两个等式，而结论是求动点(x，y)的轨迹方程，联想到平面解析几何知识，只须消去t，得到关于x、y的方程，就是所求动点的轨迹方程．

(1)设实根m，则m²+(2+i)m+2xy+(x—y)i=0，

即：(m²+2m+2xy)+(m+x—y)i=0，

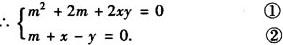
由②得m=y—x，代入①得(y—x)²+2(y—x)+2yx=0．

即(x—1)²+(y+1)²=2，轨迹是以(1，—1)为圆心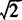，为半径的圆．

由上面解答的过程中的②知m+x—y=0可看作一条直线，由③知(x—1)²+(y+1)²=2是一个圆，因此求实根m的范围可转化为直径与圆公共点的问题．

(2)由③得圆心为(1，—1)，半径r=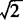，直线和圆有公共点，则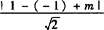≤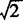，而|m+2|≤2，∴—4≤m≤0．故方程的实根的取值范围为[—4，0]．

例5 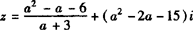(a∈R)对应的点Z①在复平面的x轴上方，②在直线x+y+7=0上．

①点Z在x轴上方，则

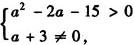
有(a—5)(a+3)>0，

∴a>5或a<—3．

②点Z在直线x+y+7=0上，

当时，

即a³+2a²—15a—30=0，

(a+2)(a²—15)=0．

∴a=—2或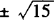时，点Z在直线x+y+7=0上．

例6 已知复数x²+x—2+(x²—3x+2)i(x∈R)是4—20i的共轭复数，求x的值．

解 根据互为共轭复数的定义，已知复数为4+20i，由复数相等的定义，可列出关于x的两个方程，这两个方程的公共解即为所求x．

因为4—20i的共轭复数是4+20i，由题意 得

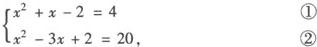
方程①的解为x=—3或x=2

方程②的解为x=—3或x=6．

∴x=—3．