时态逻辑

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第68页（2193字）

又叫做时间逻辑、时序逻辑、变化逻辑、过程逻辑等等，是研究包含时态词“过去”、“现在”、“将来”等等的命题及其推理的科学。

时态逻辑的历史最早可追溯至古希腊的麦加拉派，此后亚里士多德、阿维森那、中世纪经院学者都对此作过片断论述。第一个时态逻辑的系统是由英国逻辑学家普赖尔(A·N·Prior)在他1955年的论文《第奥多鲁的模态》和1957年的《时态与模态》一书中首先提出的。

此后时态逻辑得到了很大的发展，已成为现代哲学逻辑中十分重要的一支。

时态命题逻辑是经典命题逻辑的一个扩充，它包含经典命题逻辑的所有语言和公式，当然还要加入新的语言，例如G(将要永远)、H(曾经一直)、F(将来)、P(过去)，还有常项1(真)和O(假)；加进新的公式，例如，如果α是公式，则Gα、Hα、Fα、Pα也是公式；也要加进新的公理和推理规则，通常加入的一个规则是时间性概括规则：

。

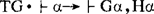常常作为时态逻辑系统的特征公理加进去的公式有：

(A₀)(a)G(p→q)→(Gp→Gq)

(b)H(p→q)→(Hp→Hq)

(c)p→GPp

(d)p→HFp

(A₁)(a)Gp→GGp

(b)Hp→HHp

(A₂)(a)Fp∧Fq→F(p∧Fq)VF(p∧q)VF(Fp∧q)

(b)Pp∧Pq→P(P∧Pp)VP(p∧q)VP(Pp∧q)

(A₃)(a)GO∨FGO

(b)HO∨PHO

(A₄)(a)Gp→Fp

(b)Hp→Pp

(A₅)(a)Fp→FFp

(b)Pp→PPp

(A₆)(a)p∧Hp→FHp

(b)p∧Gp→PGp

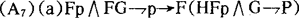
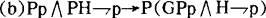
(A₈)H(Hp→p)→Hp

(A₉)(a)FGp→GFp

(b)PHp→HPp

在对经典命题逻辑(记为PC)的语言、公式、推理规则作相应的扩充之后，在PC的公理集上加入上述公式中的某些公式，就可以构造出不同的时态命题逻辑系统L，例如：

PC+A₀=L₀(极小时态逻辑K_t)

L₀+A₁a=L₁(树形时态逻辑CR)

L₁+A₂a，b=L₂(线性时态逻辑CL)

L₁+A₂b=L树(树形时态逻辑Kb)

L₂+A₃a，b=L₃(有端点线性时态逻辑)

L₂+A₄a，b=L₄(无端点线性时态逻辑SL)

L₂+A₅a或者A₅b=L₅(稠密无端点线性时态逻辑)

L₂+A₄a，b+A₅a=L_Q(稠密无端点线性时态逻辑PL)

L₂+A₆a，b=L₆

L₂+A₇a，b=L₇

L₂+A₄a，b+A₅a+A₇a，b=L_R

L₂+A₈=L₈

L₂+A₈+(p∧Gp→HO∨PG_p)=L_w

L₁+A₄a，b+A₉a，b=L₉

此外，目前正在探讨时态谓词逻辑。

时态逻辑试图把包含时态词的命题之间的推理系统化，从而为涉及时态语句的讨论精确化和推理严格化，提供语言工具和推理工具。