欧拉求和方法
书籍：方法大辞典
出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第215页（726字）
解析数论中的基本方法。
在估计和式乙an时，经常遇到an=f(n)的情形，其中f(x)是一个定义在实轴上的实函数，具有一定的光滑性，或者是单调函数。这时，欧拉求和方法常常是一个有力的工具。
欧拉求和方法的基本思想是，利用关于f(x)的积分来估计和式∑an，这个方法的基本法则如下：
(1)设当x≥a0时，f(x)是非负的增函数，则对于任何的实数a，x，x≥a≥a0，有
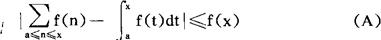
(2)设当x≤a0时，f(x)是非负的减函数，则对任何的a≤a0，极限
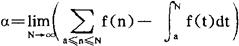
存在，而且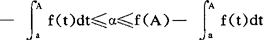
，其中A定义为：当a是整数，A=a；当a不是整数，A=〔a〕+1。此外，若f(x)还满足条件f(x)=0(1)，x→∞，则对于任何的x≥a0+1，有不等式
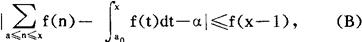
(3)设f(x)在〔a，b〕上有连续的导数，则有
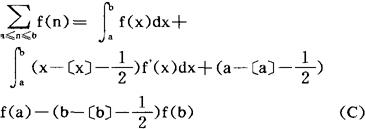
法则(A)的另一实用形式是
，其几何意义是：用曲边梯形
的面积来逼近相应的台阶形的面积
，用它便可以得到估计：当λ≥0时，
；
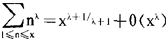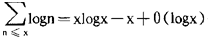等，利用法则(B)则可得到以下重要的估计：
，其中γ为欧拉常数；当σ＞1，x≥1时，
等，一般地，公式(C)称为欧拉求和公式，它是欧拉求和方法的核心，利用它可以得到许多重要的公式，例如，斯特林公式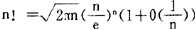
，以及黎曼ξ函数的函数方程
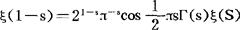，其中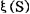
是黎曼ξ函数。