趋势预测分析法
出处：按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第955页（4751字）
为了对某一量(如产品的产量，商品的需求量等)的未来发展趋势作出预测，通常可以该量的历史数据资料——时间数列为依据，来测算它的未来趋势值。所谓时间数列(亦称时间序列)，指的是一组按时间顺序排列起来的数字序列；该序列的每一个数值通常是经观察或记录得到的，因而也称该种值为观侧值。通过分析此种规律性，就可以测算它未来的变化趋势或水平。
下面是以时间数列为依据来预测的几个常用方法。
一、移动平均法
移动平均法是最简单的时间数列预测方法。它的最主要特征是，在预测动态趋势时，不进行任何复杂的计算而只是通过连续地计算某种平均数，对时间数列的变动进行“修匀”而把动态趋势显露出来。计算平均数的方式有两种：简单移动平均法和指数移动平均法。
(一)简单移动平均法
现设Y1，Y2，…，Yn为按某种时间单位记录下来的时间数列。为方便起见，我们可以把本期的观测值(实际值)记为Yt，那么，下一期或预测期的实际值就可以用Y+1而前面各期数值用Yt－1，t－2，…，等等来表示。
简单移动平均法就是取新近数期的观测值，用该平均值作为下一期的预测值。计算公式为：
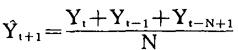
式中，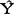
t+1——第t+1期的预测值；Yt——第t时期的实际观测值，N——用于计算平均数的数值个数，简称计算期数。
在使用公式(3．1)计算预测值时，计算期数N一经确定，就不能再变，只能是用以计算平均数的数值的交替更换。
图表3－3列出了某种商品1993年各月份的实际销售量(观测值)和按三个月与五个月计算的简单移动平均预测值。在该表里，1993年四月份的预测值17．9，就是根据1，2，3期的销售量计算得出的，即17．9=
×(17．1+18．0+18．6)，而第四栏中所示的1983年六月份的预测值17．8，是根据1，2，3，4，5期的销售量计算得出的，即17．8=
(17．1+18．0+18．6+18．5+16．9)。而对于十二月份，我们得到了按三个时期(9－11)计算的预测值19．2，和按五个时期(7－11)计算的预测值19．3。
图表3－3
在图表3－4中，我们绘制了实际销售量和两种移动平均预测值的变动线。我们看到，计算期不同，得到的预测值也不同，两种预测值的变动曲线，以按五个时期计算者较平稳，按三个时期计算的预测值变动度幅度大些。就预测来说，选择怎样的计算期数N更为合适，这需通过计算绝对平均误差(MAE=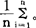
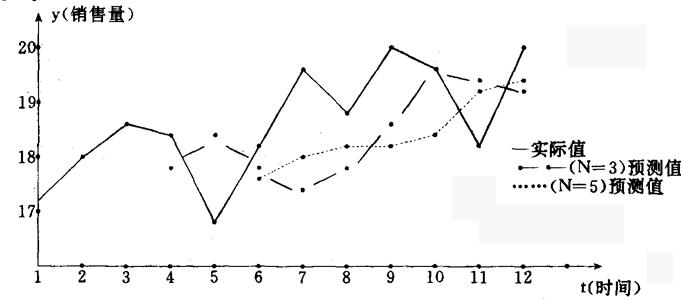
|Yi－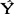
|)或平均平方误差(MSE=
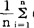Yi－
)2)来加以比较。
图表3－4
下面给出上面公式的另一种形式，它在用于连续计算各时期预测时是比较方便的。
从
t=(Yt－1+Y2t－2+…+Y1－N)／N，容易得到：
t+1=
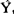t+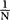
(Yt－Yt－N)
此式表明，下一期的移动平均预测值(
t+1)是本期移动平均预测值(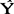
t)的调整值。
(二)指数移动平均法
在进行移动平均的预测中，常用指数移动平均法代替简单移动平均法。原因是，简单移动平均法有这样的缺点，在计算下一时期的预测值时它对最近N个时期都给予了相等的权数(1／N)，对以前的实际值所给予的权数均为0。
然而，通常认为过去各时期的观测值所包含着的未来信息是不同的，一般以最近时期为最多，也就是，近期观测值对未来时期的影响可能更大，应给予较大的权数，对于较早时期的观测值应给予递减的权数。考虑到这些情况，而制订了指数移动平均法。
指数移动平均法的着眼点与简单移动平均法类似，也是通过“修匀”历史数据的波动，而把趋势性显露出来。但计算公式稍有不同。我们仍用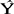
t+1表示第t+1期的预测值：
t+1=Yt+(1－a)
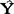t
这个等式也可写成：
t+1=
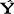t－α(Yt－
t)
我们看到，此时的预测值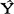
t+1为t时期观测值与其预测值t时期观测值与其预测值之差Yt－
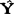t乘以指数α之和。我们也可以认为
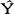t+1是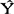
t的调整数，只不过这里用的是α乘以(Yt－Yt)而不是
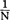乘(Yt－Yt－N，α是介于0和1之间的数。
如果将(13．2)式展开，将得到：
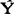t+1=αYt+(1－α)
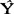t
=αYt+(1－α)〔αYt－1+(1－α)
t－1〕
=αYt+α(1－α)Yt－1+(1－α)2Yt－1
最后有，Yt+1=αYt+α(10α)Yt－1+α(1－α)2Yt－2+…
从这个等式可以看到，权数〔α，α(1－α)，α(1－α)2等〕是依次递减的，并且随着t值的增大，权数α(1－α)t将消失为0。这说明，指数移动平均公式体现了过去时期数据影响的递减性。
现用指数移动平均法对图表3－3的观测数据计算，得出图表3－5。
图表3－5
这里，最初的预测值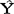
1要用Y1代替，如：
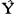2=αY1(1－α
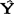1=αy1+(1－αY1。这样，在取定α的值后，便可依次按公式
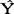t+1=
t－α(Yt－
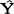t)计算。
仿照图表3－3的作法，很容易作出与图表3－2对应的图形，请读者来作。
二、指数平滑法
趋势预测法虽然比平均法考虑了趋势的变化，但是，它在利用前期的平均数和趋势平均数时，把各期的变化平均化了。实际上，近期的数列与远期的数列(或资料)对预测未来的影响是不同的。指数平滑法的基本原理是对过去不同的时期的历史数列予以不同的权数加权。则指数平滑法应用的是加权移动平均数，期愈近加权愈大，近期值越重要；期愈远，加权愈小、重要性亦越小。而趋势预测法应用移动平均数，无论期数远近，移动平均数同样重要。示意如图表3－6和3－7所示。
图表3－6
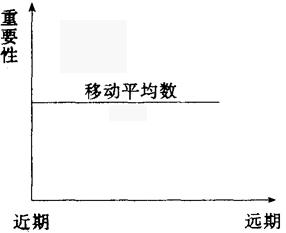
时间数列
图表3－7
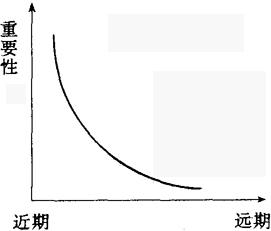
时间数列
指数平滑法通常有：单纯指数平滑法、指数加权移动平均值法、指数加权平均平滑法、采用推定量的指数平滑法，现分别介绍于下：
(一)单纯指数平滑法
它是一种以最有效地利用时间数列的最新数据(取最近一期的实绩Dt－1及最近一期的预测值Ft－1，以逐渐更新趋势，并通过指数加权(如使用平滑系数a)使最近数据得到较重份量的加权的方法。其公式为：
Ft=aDt－1+(1－a)Ft－1
式中：Ft为预测值
Ft－1为最近一期预测值
Dt－1为最近一期实绩(如销售额)
a为平滑系数
在这个公式中，a值的大小即平滑系数的大小对预测值的影响是大的。平滑系数a愈小则愈平滑，因a是对最近一期实绩进行加权的，a值愈小就使实际数占比重小，即使最近一期预测值占比重大(因a为0．1则1－a为0．9，用0．9对最近一期预测数加权故其比重大)，使预测值愈平滑。
可见，对a值的选择应十分慎重。一般应注意：(1)在正常情况下，a值取0．1～0．3；(2)当现实需求的倾向显然增大的(战争需要、一时景气、同类厂转产……)a值可取0．3～0．5，使需求倾向变动增加的实际销售量，反映在预测值上；(3)a因行业、企业、地区特点而异，各行业要分析自己的特点及客观环境，得出符合企业适用的平滑系数a。
a值的求得可用(1)试验性确定法，将a定为不同的值，通过实践检验其结果而求得；(2)试探性确定法，将a定为不同的值，绘出不同的预测图(曲线或直线)，观察其平滑性，选择a的最优值；(3)依靠监控系统自动变更a值。
公式Ft=aDt－1+(1－a)Ft－1又可改写为：
Ft=Ft－1+(Dt－1－Ft－1)
通常，在应用单纯指数平滑法时应将数据事先计算成表格，并引进一个初始值。
(二)平滑系数加权移动平均值法
此法由前公式引申而得。
∵ Ft=aDt－1+(1－a)Ft－1
∴ Ft－1=aDt－2+(1－a)Ft－2
Ft－2=aDt－3+(1－a)Ft－3
∴ Ft=aDt－1+(1－a)
｛aDt－2+(1－a)×〔aDt－3+(1－a)Ft－3〕｝=aDt－1+a(1－a)Dt－2+a(1－a)2Dt－3+(1－a)3Ft－3
或Ft=aDt－1+a(1－a)Dt－2+a(1－a)2Dt－3+a(1－a)3Dt－4+……a(1－a)n－1Dt+(1－a)nFt－n