偏摩尔量

出处：按学科分类—数理科学和化学 东北大学出版社《无机物热力学数据手册》第8页（4367字）

1．偏摩尔量

溶液中组元B_i的热力学性质与纯组元有所不同。因此引入偏摩尔量

式中 Y_i——组元B_i的偏摩尔量，它是温度、压力和浓度的函度。有的文献用表示偏摩尔量；

T——温度；

p——压力；

n_i——组元B_i的物质的量；

n_j——除B_i而外其他组元的物质的量；

Y——体系的容量性质。Y可以是体积、内能、焓、熵、亥姆霍茨自由能和吉布斯自由能。例如，偏摩尔焓为

偏摩尔熵为

体系的容量性质Y等于其中各组元的偏摩尔量与物质的量n_i的乘积之和：

对1mol溶液，上式可写为

式中 Y_m——溶液的摩尔热力学性质；

x_i——组元B_i的摩尔分数。

式(45)和式(46)都称为偏摩尔量的集合公式。

2．相对偏摩尔量

对于H_i，G_i等，由于不知道其绝对值，通常采用相对偏摩尔量。在温度、压力和溶液浓度一定时，组元B_i的偏摩尔量与纯B_i的摩尔量之差，称为相对偏摩尔量，以△Yi表之。例如：

相对偏摩尔焓

△H_i=H_i－H_i^θ (47)

相对偏摩尔熵

△S_i=S_i－S_i^θ (48)

式中H_i^θ，S_i^θ分别是纯B_i的摩尔焓和摩尔熵。

△H_i相当于下列溶解过程的焓变

B_i=〔B_i〕

方括号内的B_i表示溶于溶液中的B_i。△H_i又称为偏摩尔溶解焓(热)，单位为J·mol^－1。类似地，△S_i又称为偏摩尔溶解熵；△G_i又称为偏摩尔溶解自由能。

本书表3－1中列出了某些二元合金的相对偏摩尔量的数据。

3．混合热力学性质

溶液中各组元△H_i与x_i的乘积之总和，称为该溶液的混合焓(热)，以△H_m表之，即

有的文献称△H_i为微分混合热，把AH_m称为积分混合热。

类似地亦有混合熵和混合自由能：

式(49)至(51)均为集合公式。某些二元合金的△H_m可在表3－1中查到。该表中省略了角标“m”。

4．化学势

偏摩尔吉布斯自由能又称化学势，符号为μ_i，

纯物质的化学势就等于该物质的摩尔吉布斯自由能。μ_i是温度、压力和浓度的函数(压力对凝聚相中μ_i的影响甚小)。

1)理想气体中组元B_i的化学势用下式表示：

式中 p_i——组元Bi的分压，单位为Pa；

p^θ——标准态的压力，p^θ=101．325kPa；

R——(摩尔)气体常数；

μ_i^θ(g)——标准化学势，即当p_i=p^θ时的化学势，它是温度的函数。

对实际气体(尤其是在高压低温下)，用逸度f代替压力，组元B_i的化学势为

f_i=γ_ip_i (55)

式中 f_i——组元B_i的逸度，Pa；

y_i——逸度系数，其值体现了实际气体对理想气体的偏差程度。

当温度较高，压力较低时，实际气体的行为接近理想气体。这时γ_i→1，f_i→p_i。

2)理想溶液中组元B_i的化学势理想溶液中溶质、溶剂在全部浓度范围内都遵守拉乌尔定律：

式中 p_i——组元B_i的蒸气压；

p_i^*——纯B_i的蒸气压；

x_i——B_i的摩尔分数。

溶液中组元B_i的化学势μ_i等于与之平衡的气相(设为理想气体)中B_i的化学势，故将式(56)代入

式(53)中，得

上式等号右边前两项与浓度无关，合并为μ_i^θ，得

μ_i=μ_i^θ+RTlnx_i (58)

μ_i^θ是B_i的标准化学势，即纯B_i(x_i=1时)的化学势。它是温度和压力的函数，但实际上压力的影响很小，主要受温度影响。式(58)还可写为

△G_i=μ_i－μ_i^θ=RTlnx_i (59)

3)实际溶液中组元B_i的化学势 实际溶液不服从拉乌尔定律。为使式(58)和(59)保持其形式不变而又能适用于实际溶液，须将其中的浓度xi加以校正，即乘上一个系数γ_i，得

μ_i=μ_i^θ+RTlnγ_ix_i=μ_i^θ+RTlnai (60)

式中

a_i=γ_ix_i (61)

a_i称为组元B_i的活度；γ_i称为活度系数。γ_i＞1表示B_i对拉乌尔定律(即对理想溶液)呈正偏差；γ_i＜1为负偏差；γ_i=1则为理想溶液。式(60)中的标准化学势μ_i^θ也就是纯B_i的化学势，a_i是以纯物质B_i为标准态的活度(其它标准态参见下节)。

5．过剩函数

实际溶液中B_i的相对偏摩尔吉布斯自由能为

△G_i=μ_i－μ_i^θ=RTlna_i (62)

或

△G_i=RT1nγ_i+RT1nx_i (63)

上式右边第二项是理想溶液的相对偏摩尔吉布斯自由能，以△G_i^“表之；第一项RTlnγ_i乃是实际溶液的△G_i与理想溶液的△G_i“之差，称为B_i的偏摩尔过剩吉布斯自由能，以表之(有的文献用表示)：

的绝对值体现了实际溶液对理想溶液的偏差程度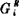；＞0为正偏差；＜0为负偏差。

1mol溶液的过剩吉布斯自由能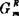是各组元的与其摩尔分数乘积之总和：

根据热力学关系式，=－S，将式(59)对T求偏导，可得理想溶液中B_i的相对偏摩尔熵为

实际溶液中B_i的相对偏摩尔熵△Si与同浓度的理想溶液中的相对偏摩尔熵之差，称为B_i的过剩熵，以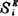表之：

形成1mol溶液的混合熵为

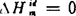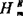因为由纯组元混合成理想溶液的过程没有热效应，即=0，，所以，实际溶液的△H_i和△H_m分别等于和，即

本书表3－1中列出了某些二元合金的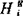，，，，和(表中已略去角标m)。只要查出其中两组数据，另一组即可算出。

〔计算实例〕 由表3－1－11中查得1400K的Cu－Sn合金在x_sn=0．3时，，=－3908J·mol^－1；又由表3－1－12中查得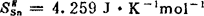，。则可算出其它的热力学函数如下：

〔计算实例〕 已知1873K的铁液中含钒为0．08%，求反应2〔V〕+3／2O₂=V₂O₃(s)的K^θ和平衡氧分压。若p_o2=101．3kPa，求反应的AG。

首先，由表2－3查得下列反应的AG^θ

2V(s)+3／2O₂=V₂O₃(s) △G^θ=－1202900+237．53T，J·mol^－1

在T=1873K时，△G^θ=－758kJ·mol^－1。若〔V〕的标准态为纯固体钒，则－758kJ·mol^－1即为所求反应的△G^θ，所以

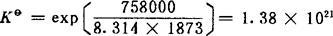
其次再由表3－2查得1873K的铁液中含钒无限稀时的活度系数的定义见式(77)〕。由于铁液含钒很低，可以认为。钒和铁的摩尔质量分别是50．94和55．85g·mol^－1，所以

av=γ_vx_v=0．1×8．77×10^－4=8．77×10^－5

将K^θ=1．38×10²¹代入上式，求得p_o2／p^θ=2．07×10^－9

∴ p_o3=2．07×10^－9×101325=2．10×10^－4Pa

当p_o2=101．3kPa时，