熵和自由能

出处：按学科分类—数理科学和化学 东北大学出版社《无机物热力学数据手册》第3页（1594字）

热力学利用熵(S)和自由能(G或F)状态函数来判断过程自发进行的方向和平衡状态。过程熵变的基本公式是

式中角注R表示可逆过程。由热力学第二定律的原理可以推出，对孤立体系，

dS≥0 (17)

“＞”适用于自发过程，“=”适用于可逆过程，在这里也就是平衡状态。

由于用熵变来判断过程的自发性要在孤立系的条件下进行，这对化学反应和相变来说不太方便，所以热力学又引入了吉布斯自由能G和亥姆霍茨自由能F两个状态函数。它们的定义是：

G=H－TS (18)

F=U－TS (19)

判断自发和平衡的公式为：

恒温恒压下，

dG≤0 (20)

恒温恒容下，

dF≤0 (21)

“＜”为自发，“=”为平衡条件。

对化学反应来说，这两个函数中，以G的应用较广，本书只讨论G的计算。G也称为吉布斯函数或自由焓，单位为J或kJ。

1．熵的计算

由热力学第三定律可知，在绝对零度(0K)时，任何纯物质完整晶体的熵都等于零，即

S₀=0 (22)

在恒压下，以δQ=C_，dT代入式(16)，并应用于标准状态下1mol的纯物质B_i，可得绝对熵(标准摩尔熵)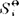与温度的关系式为：

在低温下，特别是接近绝对零度时，C，与T的关系不能用式(8)的经验式表示。通常是根据统计热力学公式，利用物质光谱数据计算出来。式中最后一项是0→298K的温度范围内所有相变过程熵变之和。本书表2－1已将由资料查出的S_iθ(298)列于表上，以298K时的S表示。298K温度以上的S_i^θ(T)用下式计算：

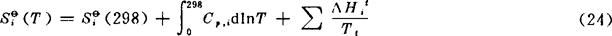
C_p，i可用式(8)代入积分，在温度间隔内有相变时，要加入式(24)最后一项的相变熵，本书每隔200K计算一个S值列于表上，当温度间隔内有相变时，其相变温度及相变熵值均已列于表上。S的单位为J·K^－1·mol^－1。

2．自由能的计算

本书所列物质B_i的自由能G_i，kJ·mol^－1，其计算公式与式(18)一致，即

G_i=H_i－TS_i (25)

由于H_i是按式(9)算出的相对值，所以Gi也是相对值。计算时单位要取得一致，S_i要将J换成kJ。表2－1已列出各相应温度的G_i值。

对于一个化学反应，如式(12)，其标准自由能变化的计算公式为：

在这里，由于H_i以单质为零而引进的相对性，在式(26)中右边加和时已经抵销，所以不影响反应△G^θ的计算。

表2－1所列化合物的G_i，与此化合物的标准生成自由能A_fG_iθ不同，它们的关系是：

式中∑v_jG_j为生成此化合物的单质G_j的代数和。

化学反应的标准自由能变化△G^θ除可按公式(26)，利用表2－1的数据计算外，还可以利用表2－3△_fG_iθ与温度的关系式△G^θ=A+BT来计算。对反应(12)，

用式(26)和式(28)计算△G^θ有时有些差别，这仅仅是由于两者所用的经验常数不同，近似程度不同所引起的。