定积分的微元法

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第101页（1619字）

若所求量U符合下列条件

(1)U是与一个变量x的变化区间［a，b］有关的量；

(2)U对于区间［a，b］具有可加性．也就是说，如果把区间［a，b］分成许多部分区间，则U相应地分成许多部分量，而U等于所有部分量之和；

(3)部分量△U的近似值可表示为f(ξ_i)△x_i，就可以考虑用定积分来表达这个量U．

具体做法

(1)根据问题的具体情况，选取一个变量．例如x为积分变量，并确定它的变化区间［a，b］；

(2)设想把区间［a，b］分成n个子区间，取其中任一子区间并记为［x，x+dx］，求出相应于这个小区间的部分量△U的近似值．如果△U能近似地表示为［a，b］上的一个连续函数在x处的值f(x)与dx的乘积，就把f(x)dx称为量U的元素且记作dU，即

dU=f(x)dx；

(3)以所求量U的元素f(x)dx为被积表达式，在区间［a，b］上作定积分，得，即为所求量U的积分表达式，这个方法通常叫做元素法或微元法．

应用方向 平面图形的面积，体积，平面曲线的弧长，功，水压力，引力和平均值等．

通过两个例子说明微元法在物理上的应用 由物理学知道，如果物体在作直线运动的过程中有一个不变的力F作用在这物体上，且这个力的方向与物体的运动方向一致，那么，在物体移动了距离s时，力F对物体所做的功为W=F·s．

如果物体在运动的过程中所受的力是变化的，就不能直接使用此公式，而需采用“微元法”思想．

例1 有两个质量分别为m₁，m₂的质点A，B，相距为a．将质点B沿其AB方向移动到点C，B与C之间的距离为l，求A与B之间引力所做的功(见图7．1)．

图7．1

解 取坐标系如图7．1所示，选积分变量为x∈［a，a+l］，任取子区间［x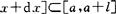，，则在子区间上功的微元为

dW=Fdx，

其中，则引力所做的功为

由物理学知道，在水深为h处的压强为p=γh，这里γ是水的比重．

如果有一面积为A的平板水平地放置在水深为h处，那么，平板一侧所受的水压力为P=pA．如果平板垂直放置在水中，由于水深不同的点处压强p不相等，平板一侧所受的水压力就不能直接使用此公式，而需采用“微元法”思想．

例2 一个横放着的圆柱形水桶，桶内盛有半桶水，设桶的底半径为R，水的比重为γ，计算桶的一端面上所受的压力(见图7．2)．

图7．2

解 取坐标系如图7．2所示，选积分变量为x∈［0，R］，任取子区间［x，，则在子区间上小矩形片的压力微元为

端面上所受的压力为