向量的坐标表达式及其有关问题

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第114页（665字）

向量的坐标表达式 设向量a的起点为M₁(x₁，y₁，z₁)终点为M₂(x₂，y₂，z₂)，则

=｛x₂－x₁，y₂－y₁，z₂－z₁｝．

其中，i，．j，k分别为x，y，z轴上与轴的正方向相同的单位向量，称为基本单位向量．

当起点在原点，终点为(x，y，z)时向量a为

a=xi+yj+zk=｛x，y，z｝．

向量的长度公式 设向量a=xi+yj+zk，则

设M₁(x₁，y₁，z₁)，M₂(x₂，y₂，z₂)则

向量的方向余弦 设α，β，γ为向量a与x，y，z轴的正方向夹角不超过π的角，则称α，β，γ为向量a的方向角．方向角的余弦称为向量a的方向余弦．

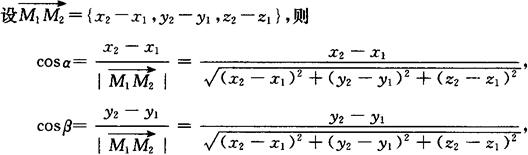
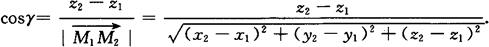
设a=｛x，y，z｝，则

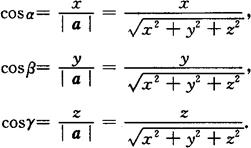
方向余弦之间的关系 cos²α+cos²β+cos²γ=1．