二元函数的泰勒公式
书籍:数学手册(大学生用)
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第159页(928字)
定理 设z=f(x,y)在点(x0,y0)的某一邻域有直到n+1阶的连续偏导数,(x0+h,y0+k)为此邻域内任一点,则二元函数f(x,y)在点(x0,y0)的n阶泰勒公式为
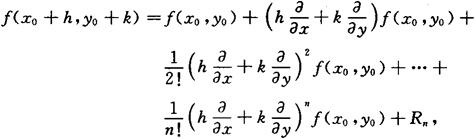
其中
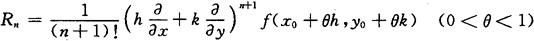
称为拉格朗日型余项.记号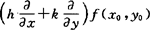 表示
表示
hfx(x0,y0)+kfy(x0,y0),
(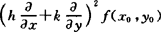 表示
表示
h2fxx(x0,y0)+2hkfxy(x0,y0)+k2fyy(x0,y0).
一般地,记号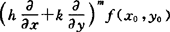 表示
表示
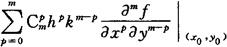
误差估计式
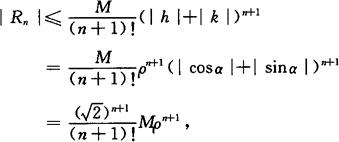
其中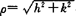 ,M为函数z=f(x,y)在点(x0,y0)处的(n+1)阶偏导数的界.
,M为函数z=f(x,y)在点(x0,y0)处的(n+1)阶偏导数的界.
误差|Rn|是当ρ→0时比ρn高阶的无穷小.
当n=0时,由二元函数f(x,y)在点(x0,y0)的n阶泰勒公式就是二元函数的拉格朗日中值公式:
f(x0+h,y0+k)=f(x0,y0)+hfx(x0+θh,y0+θk)+kfy(x0+θh,y0+θk).
推论 如果函数f(x,y)的偏导数fx(x,y),fy(x,y)在某一邻域内都恒等于零,那么函数f(x,y)在该区域内为一常数.
二元函数n阶麦克劳林公式 在二元函数f(x,y)在点(x0,y0)的n阶泰勒公式中,若取x0=0,y0=0,则得n阶麦克劳林公式:
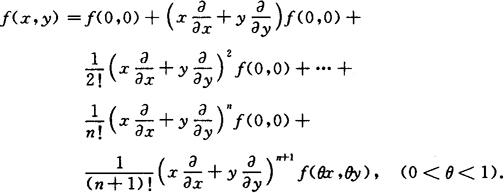
上一篇:多元函数的极值和最大(小)值
下一篇:数学手册(大学生用)目录