一阶微分方程的可积类型

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第231页（3703字）

可分离变量的微分方程 形如

M(x)M₂(y)dx+N1(x)N₂(y)dy=0

的方程称为可分离变量的微分方程，其中M₁(x)，M₂(y)，N₁(x)，N₂(y)均为已知表达式．

求解方法：把变量x，y分离到两边后再积分，即

齐次方程(或齐次型方程) 形如

的方程叫做齐次方程，f为已知．

求解方法：

令，则y=xu，y′=u+xu′，代入原方程得

u+xu′=f(u)

分离变量后即可积分．

一般的齐次方程 形如

的方程称为齐次方程．

求解方法：

(1)当0时，将坐标平移到新原点O′(a，b)．令

x=X+a，y=Y+b，

原微分方程即可化为齐次方程，其中a，b是

的解．

v=a₁x+b₁y

即可解得．

例 解微分方程(2x+y－4)dx+(x+y－1)dy=0的通解．

解 由

解得O′(3，－2)．令x=X+3，y=Y－2．原方程成为

(2X+Y)dX+(X+Y)dY=0．

解得．

再换回原变量，得通解．

一阶线性微分方程

形如

的方程叫做一阶线性微分方程，P(x)，Q(x)为已知函数．

当Q(x)恒为0时，

叫做一阶齐次线性微分方程．

当Q(x)不恒为0时，

叫做一阶非齐次线性微分方程．

求解方法

(1)齐次线性微分方程

分离变量得到

从而得

或

(2)非齐次线性微分方程

通解为

(3)一阶非齐次线性微分方程的常数变易法

设一阶非齐次线性微分方程的解为

其中u=u(x)是待定函数，代入一阶非齐次线性微分方程，解得，

即得原方程的通解．

伯努利(Bernoulli)方程 形如

的方程称为伯努利方程．

求解方法：令z=y^1－n，则

代入原方程得线性方程

全微分方程 将一阶微分方程写成

P(x，y)dx+Q(x，y)dy=0．

如果它的左端恰好是某一个函数u=u(x，y)的全微分，则该方程叫做全微分方程，其通解为u(x，y)=C．

求解方法：

例 求解e^ydx+(xe^y－2y)dy=0．

解 因P(x，y)=e^y，Q(x，y)=xe^y－2y．则

所以该方程为全微分方程，由

两边积分得

u(x，y)=xe^y+C(y)，

又已知

由(1)，(2)得

C_′(y)=－2y，

因此 C(y)=－y²+C₁，

所以 u(x，y)=xe^y－y²+C₁．

通解为

xe^y－y²=C(C=－C₁)．

方法2

后一个积分中将x视作常数．方程通解为

u(x，y)=C，

即

积分因子 若在方程

P(x，y)dx+Q(x，y)dy=0

中，．如果方程两边乘以因子μ(x，y)后成为全微分方程，即μ(x，y)P(x，y)dx+μ(x，y)Q(x，y)dy=0为全微分方程，则称μ(x，y)为积分因子

通常可考虑作为积分因子用的有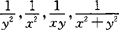等．

如方程ydx－xdy=0不是全微分方程，两边乘上后，

就是全微分方程．

一阶微分方程解的存在与惟一性定理 如果f(x，y)在点(x0，y0)处的一个邻域内连续，则微分方程y′=f(x，y)总存在满足初始条件y|_x=x0=y0的解．如果在这个邻域内也是连续的，则解是惟一的．

正交轨线

(1)一阶微分方程的通解含有一个任意常数，它是一个单参数曲线族；反过来，单参数曲线族一般也可以看成一个一阶微分方程的通解．

(2)求单参数曲线族的微分方程的方法

设单参数曲线族的方程为

Q(x，y，C)=0，

其中C为任意常数．两边对x求导，得

φ′x+φ′yy′=0．

如果上式不含有任意常数C，则上式就是该单参数曲线族所满足的微分方程；如果含有任意常数C，则需从下列方程组中消去C，才能得到该单参数曲线族的微分方程

例 求曲线族(x－c)²+y²=1的微分方程．

解 两边对x求导，得

2(x－c)+2yy′=0．

与原方程联立，消去c，得

(yy′)²+y²=1，

即为所求的微分方程．

(3)正交轨线

设两族曲线在每一个交点(x，y)上两条切线垂直，则微分方程F(x，y，y′)=0的正交轨线必满足．解此微分方程就得原方程的曲线族的正交轨线方程．

例 求曲线族x²+y²=C的正交轨线族方程．

解 x²+y²=C的微分方程为．它的正交轨线族的微分方程为，解得正交轨线族方程为y=kx．