随机变量的数学期望

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第409页（1755字）

数学期望就是随机变量的按照概率规律求出的加权平均值．

一维随机变量的数学期望E(X)

1．离散型随机变量

①有限型：若X的分布律为P｛X=x_i｝=p_i，i=1，2，…，n，则X的数学期望为．

②无限型：P｛X=x_i｝=p_i，i=1，2，…，

如果级数绝对收敛，则X的数学期望为

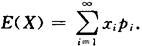
2．连续型随机变量

设X的密度函数为f(x)，如果广义积分绝对收敛，则X的数学期望为

二维随机变量的数学期望

1．离散型随机变量

设(X，Y)的联合分布律为P｛X=x_i，Y=y_i｝=p_ij．两个边缘分布律分别为

P｛X=x_i｝=p_i．，P｛Y=y_i｝=p_．j，

则X，Y的数学期望分别为

2．连续型随机变量

设(X，Y)的联合密度函数为f(x，y)，边缘密度函数分别为f_X(x)，f_Y(y)，则X，Y的数学期望分别为

函数的数学期望

1．一维随机变量

若Y=g(X)，E(Y)=E［g(X)］．

(1)离散型随机变量

设X的分布律为P｛X=x_i｝=p_i，则Y的数学期望为

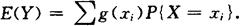
(2)连续型随机变量

设X的概率密度函数为f(x)，则Y的数学期望为

2．二维随机变量

若Z=g(X，Y)，E(Z)=E［g(X，Y)］．

(1)离散型随机变量

设(X，Y)的联合分布律为P｛X=x_i，Y=y_i｝=p_ij，则Z的数学期望为

(2)连续型随机变量

设(X，Y)的联合密度函数为f(x，y)，则Z的数学期望为

数学期望的性质(假设期望存在)

(1)若C为常数，则E(C)=C．

(2)若a为常数，则E(aX)=aE(X)．

(3)E(X±Y)=E(X)±E(Y)．

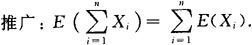
(4)若X，Y独立，则E(XY)=E(X)E(Y)．

推广：若X1，X2，…，Xn相互独立，则