财务预测的方法
出处:按学科分类—经济 企业管理出版社《现代企业理财手册上》第311页(8960字)
财务预测的具体方法有很多,归纳起来有两类,定性预测法和定量预测法。
1.定性预测法
这类方法的特点是依靠熟悉业务及经验丰富的内行和专家,凭借经验和判断能力,对企业财务状况的未来发展趋势和变化方向作出判断和估计的一类预测方法。
这类方法主要有以下几种形式:
(1)经验判断法
这种方法就是靠熟悉业务、具有丰富经验和综合分析能力的人员来进行预测的一种方法。运用经验判断法进行预测,可以先提出一些指定的问题,把有经验的人员主要是财务业务骨干领导找来座谈,征求他们对这些问题的意见,然后再综合归纳,做出预测。
(2)调查法
这种方法就是根据预测的目的、要求,通过调查,取得必要的资料,然后进行加工整理和分析研究,并据以进行预测的一种方法。这种方法经常采用的形式是走访用户,召开有关人员参加的招待会,电话咨询等。
2.定量预测法
定量预测就是根据收集的数据资料运用一定的数学方法进行科学的加工整理,并建立数据模型,借以揭示有关变量之间的规律性联系,用来预测和推测未来财务活动发展变化情况的一种预测方法。
定量预测经常使用的技术主要有以下方法:
(1)时间序列预测法
它是根据某项指标按时间顺序排列的历史财会数据,运用一定数学方法进行加工、整理、找出其发展规律,据以预测未来发展趋势的一种方法。
影响时间序列预测值的因素有:
a.长期趋势:是一种在较长时间内预测值呈渐增或渐减的现象。
b.循环变动:是一种以一年以上较长时间为周期的反复变动。
c.季节变动:是一种以一年为周期的反复变动。
d.偶然变动:是一种不规则的变动,其发生的原因主要是天灾,人祸等突然发生的事故所致。
这种方法大中企业使用较多,其采用的技术方法通常使用简单平均法、移动平均法、加权移动平均法、指数平滑法。
a.简单平均法。即根据过去若干时期的数值,求简单算术平均数作为未来的预测数。它的计算公式如下:

公式中:A——简单平均数
D1+D2+……+Dn——过去若干期的数值
n——期数
例:某企业本年1~4月销售量如下:

根据上述资料,可预测以后每月销售量如下:

简单平均法是将过去的差异平均化,它适用于各月基本稳定的指标,
b.移动平均法。同样是根据过去若干期实际发生资料,求其平均数,但时间上不断往后移,它的计算公式如下:

公式中的A——移动平均数
Dt——各期销售量
n——期数
例:上述资料取前5个月数据求为期2个月的移动平均数:
预计4月份销售量=(1,000+1,100+1,050)÷3=1,050(件)
预计5月份销售量=(1,100+1,050+1,200)÷3=1,117(件)
预计6月份销售量=(1,050+1,200+1,250)÷3=1,167(件)
移动平均法同样是使各月差异平均化,但时期选择上尽可能接近预测月份,使预测更接近于实际。
c.加权移动平均法。根据过去若干时期实际发生的资料,时间上不断往后移动,并按其与预测期的远近进行不同的加权,求其平均数,它的计算公式如下:

公式中:A——移动加权平均数
Dt——各期销售量
Ct——权数
n——期数
上述资料取前5个月数据求为期3个月的加权移动平均数如下:
预测4月份销售量=(1,000×1+1,100×2+1,050×3)÷(1+2+3)=1,058(件)
预测5月份销售量=(1,100×1+1,050×2+1,200×3)÷(1+2+3)=1,133(件)
预测6月份销售量=(1,050×1+1,200×2+1,250×3)÷(1+2+3)=1,200(件)
它适用于各月销售量波动较大的产品。
d.指数平滑法。它是根据历史资料和数据(包括上期实际和上期预测数),用指数加权的办法来进行移动平均的方法。计算如下:
Ft=a(Dt-1)+(1-a)Ft-1
公式中:Ft——本期预测数
a指数(或称平滑系数)(0<a<1,a值大小可根据实际来决定,一般近期影响大,a也大,但不超过0.5)
Dt-1——上期实际数
Ft-1——上期预测数
即:
本期预测数=上期实际数×指数+上期预测数×(1-指数)
取上述前5个月的数据列出期预测计算结果如下:

(2)相关因素预测法
它是根据某项指标与其他指标之间内在的相互依存、相互制约的关系,建立相应的数学模型,寻求其发展变化的规律,进而根据已知测定未知,根据过去预测未来的一种方法。主要有回归分析预测法、量本利分析预测法等。
a.回归分析法。它是通过研究已知数据资料,从中寻求这些数据资料演变因果规律的一种数理统计方法。
企业通常情况下多采用一元线性回归分析预测法。一元线性方程的通式为:
Y=a+bx
式中x为自变量,Y为因变量,a、b为回归系数。
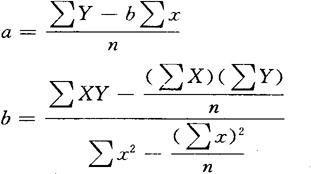
在销售预测中x代表年份,Y代表销售量。由于销售预测中自变量X比较简单,以1递增,因此,可以采用简单的方法,令Σx=0,则计算公式可简化为:

若n为奇数,则取x的间隔期为1,将x=0置于预测基础期的中间;若n为偶数,取x的间隔期为2,将x=1和x=-1置于基础期中间的上下两期。
例:某企业1980~1985年的销售量如下:


代入公式

预测1986~1990年销售量如下:
86年:Y=1,150+44.29×7=1,460(件)
87年:Y=1,150+44.29×9=1,549(件)
88年:Y=1,150+44.29×11=1,637(件)
89年:Y=1,150+44.29×13=1,726(件)
90年:Y=1,150+44.29×15=1,814(件)
回归直线本身包括一定的误差,为了判定预测数的可靠程度及其范围,可以计算标准差δ如下:
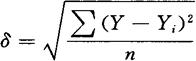
这里的yi,可以用各年的预测数或实际平均数,现计算有关数据如下:

代入公式

在正态颁下,1986年预测实现范围,在1,460±79,即在1,381~1,539件的可能性为68.3%,在1,460±79×2,即在1,302~1,618件的可能性为95.5%。这样,可以对销售预测实现可能性做到心中有数了。
b.量本利分析预测法
量本利分析预测法就是利用成本、销售和利润三个因素之间的关系,对其中某一因素进行预测的一种方法。这种方法在实际工作中主要用于以下几个方面:确定企业保本时的销售量;预测在一定销售量时所能获得的利润;计算要达到一定的目标利润时所需的销售量;在降低销售价格和增加销售数量之间进行决策,能使企业获得较好的经济效益。
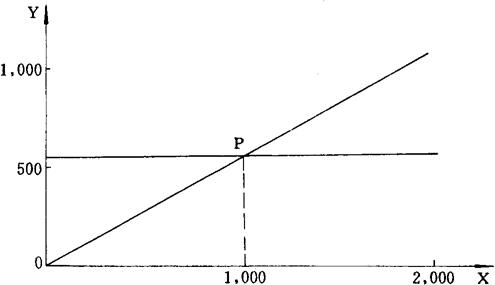
盈亏平衡点
是指在坐标图中,企业销售线与总成本线的交叉点,也就是企业既无盈利也不亏损的点,超过这一平衡点总收入与总成本的差额即为企业的盈利,若低于这一平衡点总收入与总成本的差额即为企业的亏损点。
预测盈亏平衡点很关键,对于预测企业生产销售量水平,目标利润,价格决策等方面内容都有很大作用。确立该平衡点的方法有以下几种方法:
第一,生产量(或销售量)法
生产量(销售量)法,就是以某一产量的固定费用和变动费用,与同一销售量的销售收入进行比较,以确定盈亏平衡点的方法。
a.作图法
以生产量(销售量)为横坐标,生产总费用(销售总收入)为纵坐标构成直角坐标系。先在纵坐标中截取F值于C点,作横坐标的平行线AC(固定费用线);然后以C点为起点,按Y=F+V·X的方程式作生产费用线CD(合成成本线);再从原点开始,按S=Q·X方程式作销售收入线OB;生产费用线OD和销售收入线IB的交点P,即为盈亏平衡点(保本点)。P点的横坐标x1,即为保本生产量(销售量)。所作之图,就是上述标准式盈亏分析图。
b.计算法
根据盈亏分析图,可见:
S=Q·x
Y=F+V·x
在盈亏平衡点P时,S=y
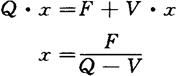
例:某厂生产甲产品,全月的固定费用为3,000元,甲产品的单位变动费用60元,单位售价100元,当甲产品生产多少时,销售收入才能和销售成本相等?
已知:F=3,000元,V=60元,Q=100元。
求:x1=?
解:
验证:S=Q·x=100×75=7,500(件)
Y=F+V·x=3000+60×75=7500(元)
第二,销售额法
销售额法是以某一销售额的固定费用和变动费用,与销售额本身进行比较,以确定盈亏平衡点的方法。
a.计算法
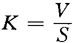
式中:K——费用变动率
V——变动费用总额
S——销售收入总额

设盈亏平衡点的销售额为S1,当在盈亏平衡点时,则:

式中:S1——盈亏平衡点的销售额
F——固定费用总额
V——变动费用总额
S——销售总收入
例:某厂甲产品计划销售额为10,000元,计划固定费用总额为3,000元,计划变动费用为6,000元,当甲产品的销售额为多少时,才能与销售成本相等?
已知:S=10,000元,F=3,000元,V=6,000元。
求:S1=?
解:


这里使用的仍是上例。销售额7,500元的销售量为75件,故盈亏平衡点的计算结果与上法相同。
b.作图法
纵坐标表示费用和利润,横坐标表示销售额,并用同一刻度。
以45°作OB线,为销售额线。
以固定费用3,000元作CA线,为固定费用线。
以销售额为10,000元时的F+V定D点,连CD,CD为全部成本线。
OB线和CD线的交点P,即为盈亏平衡点。
第三,边际收益法
边际收益是指销售收入减去变动费用后的余额,即固定费用加销售利润。计算公式是
M=S-V=F+P
式中:
M——边际收益
S——销售收入
V——变动费用
F——固定费用
P——销售利润
边际收益法适合于研究多品种生产的盈亏平衡点。
a.作图法
例:某企业有下述资料:

按表列资料计算各产品的边际收益率(m)。

再按边际收益率由高至低顺序排列,并计算销售收入累计和边际收益累计。结果如下:

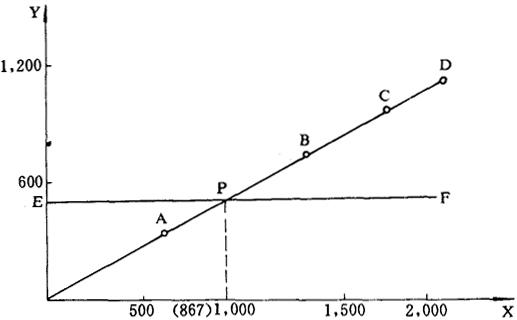
根据上表作图:
用纵坐标(y)表示边际收益和固定费用,横坐标(x)表示销售收入。标明刻度。
取丁产品的销售收入600元和边际收益350元之点为A,连OA。
取丁产品和甲产品的销售额之和600+700=1,300元,与丁产品和甲产品的边际收益之和350+400=750元,定B点,连AB。
依此类推,分别求得C点和D点,连成OABCD折线。此线为四种产品的边际收益折线。
在y轴上截OE=固定费用500元,过E作x轴的平行线EF。此线为固定费用线。
折线OABCD与EF的交点P,即为盈亏平衡点。在本例中,P点对应的销售额为867元。
b.计算法
计算盈亏平衡点所在产品区。
首先按各产品的边际收益率m由高到低顺序排列,并顺序计算边际收益的累计值,然后顺序用M累计数与F比较。在比较过程中,当M累计数首先大于F时,则新计入M值的产品,就是P点所在的产品区。
在本例中,丁产品和甲产品的边际收益之和为750元,大于固定费用500元,故甲产品就是盈亏平衡点P所在的产品区。
计算与P对应的销售额。
设P所在产品区的产品序号为n,则:

在本例中,P点在甲产品区。则:
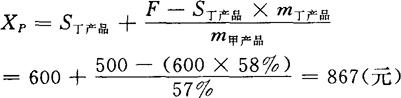
利用边际收益法计算产品盈亏平衡点的销售额,也可用多品种生产的计算公式。在单品种生产条件下,盈亏平衡点的产品区只有一个,故P点所在产品区的序号n=1。公式中的n-1=0,因而公式中

例:某产品的固定费用为560元,当销售收入为2,000元时,边际收益为1,120元,该产品盈亏平衡点的销售额是多少?
已知:F=560元,S=2,000元,M=1,120元。
求:Xp=?
解:

验证