木片料仓锥底的选取计算

出处：按学科分类—工业技术 中国轻工业出版社《制浆造纸工业计算手册上册》第18页（1774字）

【说明】锅顶料仓的锥底有四角锥形和圆锥形两种。四角锥形可以利用四壁作梁，在结构上比较合理，而且建筑体积的利用比较经济，在外形体积相同的情况下容积较大。这样，可以降低楼层高度。但缺点是下料比较困难。因此，在设计时必须掌握锥底棱边(AE)与水平面(ABCD)的空间夹角α与休止角β保持下述式中关系，这样，就可以保证料片沿着仓壁下滑，见图1－1－5。

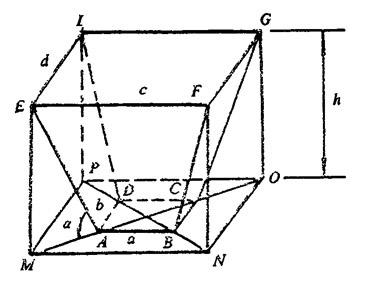
图1－1－5 料仓四角锥底空间角度的关系

1．α与β的关系

【公式】

式中 α——空间夹角(度)

β——休止角(度)，即料片不会进行自然滑动时最大的α角

2．α角的选取计算

①出料口为长方形时

【公式】

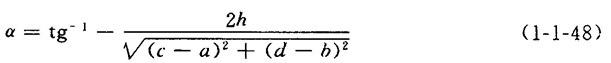
式中 h——上下口高(mm)

c、d——上口尺寸(mm)

a、b——下口尺寸(mm)

②出料口为正方形时

【公式】

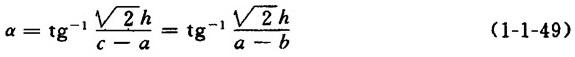
③休止角的常取值

【说明】一般取木片堆积角(休止角)β=45°

故 α≥β+3°=48°

【注意】最后确定α角时，尚需考虑料仓结构与进出口设备的联接关系以及料片对仓壁斜面之间的摩擦力等因素。

3．底锥侧面ABEF与平面ABCD的夹角β₁的计算

①出料口为长方形时

【公式】

式中符号含义及单位均同式1－1－48

②出料口为正方形时

【公式】

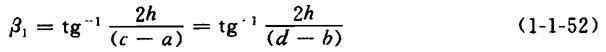
式中符号含义及单位均同式1－1－48

4．底锥侧面BCFG与平面ABCD的夹角β₂的计算

①出料口为长方形时

【公式】

②出料口为正方形时

【公式】

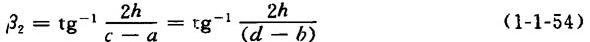
以上两式中符号含义及单位均同式1－1－48

5．α与β₁β₂的关系

【说明】当出料口为正方形时，α与β₁及β₂之间保持以下关系，这样，α及β角均符合要求。

【公式】

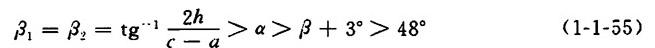
【例】设底锥下口尺寸a=b=760mm，上口尺寸c=a=3000mm 上下口高h=1800mm，试论证料仓的设计是否符合要求。

解：

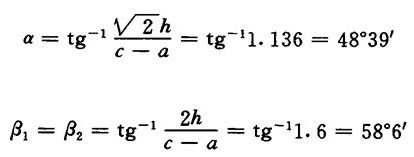
故 β₁=β₂〉α〉48°，满足设计要求。