叶片式摆动液压缸设计要点
出处:按学科分类—工业技术 北京理工大学出版社《新编液压工程手册下册》第1581页(2889字)
(1)用转矩公式确定主要结构尺寸
通常情况下,负载在空气或水中工作,其粘性阻尼系数可以忽略。输出转矩只要克服驱动负载所必需的转矩和使负载获得必要的角加速度所需的转矩。即:

式中 TL——负载转矩(N·m);
I——包括输出轴(叶片轴)本身惯量在内的转化到输出轴上的总转动惯量(kg·m2);
ω——负载的角速度(rad/s)。
TL主要包括两部分,即负载摩擦力矩和由负载重量引起的转矩,都能从已知的工况求得。在输出轴尺寸和材料尚未确定前,I值难以求得。因为输出轴本身的转动惯量与总惯量相比通常都很小,在初步设计时可把它忽略。通常负载又直接与输出轴相连,中间没有变速机构,因此这时的总转动惯量就是负载折算到输出轴上的惯量,I值就不难求得了。ω的大小及其随时间变化的规律是已知的。这样,由式(25.5-1)就可求取T。从表25.5-1中知输出转矩公式:

式中的符号意义及其单位见表25.5-1。
严格来说,由式(25.5-1)求取的T值比式(25.5-2)的T值要小些。但初步确定结构尺寸时可视为相等。这样,先设Z=1,ηm=0.8~0.9。通常进、出口压力已知,再按安装空间大小设定b、D、d三个尺寸中的两个,就能按式(25.5-2)求得另一个尺寸。三个初定的尺寸应进行圆整。D值向大的方向圆整,d值向小的方向圆整。b若不能取整数,可取到小数后一位。这样求出的尺寸若不宜,三者间可再调整直到满意为止。如所需转矩较大,摆角在100°左右,可考虑采用双叶片式结构。此时Z=2,ηm值取0.9~0.95。若摆角在60°左右,结构允许时也可采用三叶片式,即Z=3。但此情况不多。
当进、出口压力需自选定时,首先要考虑整个液压系统的要求。出口压力能选定零最好。进口压力选高一些能使摆动液压缸体积小,重量轻,但要密封性好。既无外泄漏又使内泄漏尽量小。
上述方法确定尺寸有时要反复几次才能取得满意的结果。但实践证明是比较实用。
(2)校核输出转矩
各结构尺寸确定后,再按式(25.5-2)求出较为精确的输出转矩。选定输出轴的材料以后,其惯量也可求出。代入式(25.5-1)就能得负载实际所需转矩。对按不同公式算出的转矩进行比较,可知最后选定的结构尺寸是否合理。需要强调的是输出转矩必须略大于实际所需转矩。
(3)求为达到负载角速度ω所需的输入流量
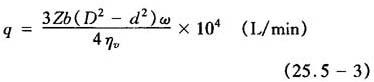
式中的符号意义及其单位见表25.5-1。
影响容积效率ηv的因素较多。但主要是通过叶片密封部位的内泄漏。密封形式和材料、油的运动粘度、叶片的角速度和工作压力都会影响内泄漏的大小。尤其是工作压力升高时,内泄漏会迅速增加。单叶片式的内泄漏大体如图25.5-1。由图可知:油的运动粘度不变时,对于同一个摆动液压缸,工作压力大者内泄漏大。若工作压力也一定,则排量大的摆动液压缸内泄漏也大。

图25.5-1 单叶片式摆动液压缸的内泄漏
表25.5-1列出了各类摆动液压缸的机械效率和容积效率的选取范围。
(4)主要零件的强度和刚度计算
(A)缸盖和缸体都受内压连续均布载荷时,其强度和刚度可根据具体的几何形状参照弹性薄板或薄壳的有关公式计算。若摆角在300°左右,摆动液压缸形状成短圆柱状时,也可参照液压缸缸筒的办法进行计算。
(B)对于片状结构的叶片,其危险截面在根部。最大正应力为

式中 T——叶片根部所受弯矩,由下式求得

W——叶片根部抗弯截面系数,对矩形截面
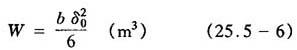
D——缸体内径(m);
d——叶片安装轴外径(m);
p1——进口压力(MPa);
p2——出口压力(MPa);
δ0——叶片根部厚度(m)。
式(25.5-5)和式(25.5-6)中的b为叶片轴向宽度(m)。
应该使

式中 σs——叶片材料的屈服极限(MPa);
n——安全系数,取3~4。
为降低应力集中系数,叶片根部和输出轴的连接处应尽可能加大过渡部分的圆角。
对于块状结构的叶片,可用式(25.5-5)进行强度计算。
(C)缸体连接计算:缸体和缸盖通常都用螺栓连接。其强度要按拉应力和剪应力的合成应力计算。可参见第23章液压缸的有关部分。应该注意的是摆动液压缸的内腔常呈环式扇形,所以其最大拉力应是缸内最大压力和缸盖上最大受力面积之乘积。
(D)输出轴:单叶片式的输出轴不仅在承受最大扭矩时要有足够的强度,而且在承受径向载荷时也应有足够的刚度。如果径向载荷引起的弯矩较小,可采用许用扭应力计算法来考核轴的强度。双叶片式的输出轴不受径向载荷,所以也可用此法计算。
摆角大、工作压力又高的单叶片式摆动液压缸,因轴上所受不平衡径向力很大,故对输出轴的弯曲变形也应验算。其挠度应在允许范围内。通常许用挠度可取轴支承间距的万分之二。