电液位置控制系统

出处：按学科分类—工业技术 北京理工大学出版社《新编液压工程手册下册》第2067页（2920字）

设有一数控机床工作台的位置需要连接控制，其技术要求

指令速度信号输入时引起的速度误差为

e_v=5mm

干扰为位置输入时引起的位置误差

e_pf=±0．2mm

给定设计参数为

工作台质量 m=1000kg

最大加速度 a_max=1m／s²

最大行程 S=50cm

最大速度 v=8Cm／s

工作台最大摩擦力 F_f=2000N

最大切削力 F_c=500N

供油压力 p_s=6．3MPa

反馈传感器增益 K_f=1V／cm

确定系统的主要参数。

(1)确定系统方案

采用图34．4－1的伺服阀控制液压缸的系统结构。

图34．4－1 伺服阀控制液压缸系统

(2)确定工作台速度和负载力的关系

负载力由切削力F_c摩擦力F_f和惯性力F_a等组成。惯性力F_a按最大加速度考虑

F_a=ma_max=1000N

系统在最恶劣的负载条件下工作时的总负载力F=3500N。工作台速度和负载力的关系曲线如图34．4－2所示。

图34．4－2 工作台速度和负载力的关系曲线

(3)确定液压缸有效工作面积A和结构尺寸D，d令负载压力，因为F=Ap_L，所以

现确定液压缸活塞直径D及活塞杆直径d。因为，取d／D=0．5代入上式得

D=3．75cm，圆整取D=4cm，d=2．2cm

校核有效工作面积A得 A=8．04cm²，取A=8cm²。

(4)确定伺服阀规格

最大速度工况时负载压降为MPa

伺服阀压降△p_v=p_s－p_L=1．925MPa

负载流量q_L=v_m×A=3．84L／min

查伺服阀样本，阀压降7MPa，额定电流I_R为30mA时，流量为8L／min的伺服阀就可满足p_v=1．925MPa，输出流量q_L＞3．84L／min的要求。

(5)确定系统传递函数

伺服阀控制液压缸系统的方块图如图34．4－3所示。

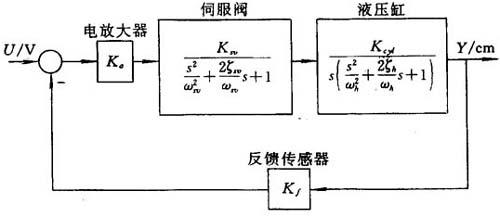
图34．4－3 伺服阀控制液压缸系统方块图

(A)电液伺服阀的传递函数

额定流量8L／min的伺服阀在供油压力p_s=6．3MPa时的空载流量为7．6L／min，阀的增益为

伺服阀生产厂提供了ω_sv=600rad／s，ζ_sv=0．5的数值。

电液伺服阀的传递函数

(B)液压缸的传递函数

设β_e=700MPa，V_t=A×S=400×10^－4m³

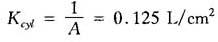
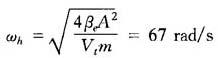
取K_ce=0．0258cm⁵／s·N，代入ζ_h式中得

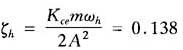
所以得到液压缸的传递函数为

(C)反馈传感器的传递函数

G_f(s)=1V／cm

(D)电放大器的传递函数待定

G_a(s)=K_a

(E)系统的开环增益

K_v=K_aK_svK_cylK_f

=K_a×4216×0．125×1=527K_a

根据系统判别稳定条件2ζ_hω_h=0．276ω_h，K_v应＜2ζ_hω_b，取K_v=0．25ω_h=17rad／s代入前式得

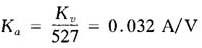
(6)系统波德图

绘制的系统波德图如图34．4－4所示。

图34．4－4 系统波德图

从图中可见，系统频宽f_－3dB时，稳定裕量为5dB和90°。

(7)计算系统稳态误差

·指令输入最大速度v=8cm／s时的误差为

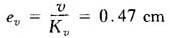
·干扰输入引起的误差：干扰有伺服放大器温度零飘、伺服阀的零飘和磁滞及执行元件的不良灵敏度等，将其总和折合成伺服阀输入电流的干扰为f=±0．02I_R，对这个干扰来说，系统属于O型，当其在一段时间内为常量时，系统的位置误差为

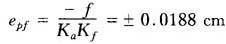
可见，系统达到了原定设计指标。