z变换
出处:按学科分类—工业技术 北京理工大学出版社《新编液压工程手册上册》第169页(1925字)
(1)z变换定义
采样信号与连续信号之间的关系为

对上式两端取拉氏变换,得

令z=eTs,则式(5.7-8)可写成

X(z)称采样信号x*(t)的z变换。以 [x*(t)]表示对x*(t)进行z变换,有时也使用符号
[x*(t)]表示对x*(t)进行z变换,有时也使用符号 [x(t)],但其含义仍然是对其采样信号进行z变换。
[x(t)],但其含义仍然是对其采样信号进行z变换。
(2)z变换表
常用时间函数的z变换和拉氏变换列于表5.7-1。
表5.7-1 常用时间函数的z变换


(3)z变换的基本定理
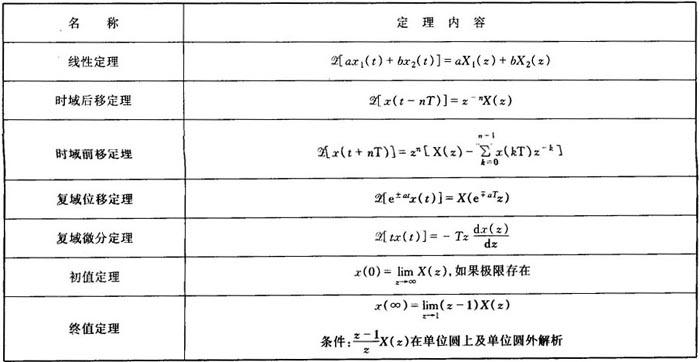
常用的z变换的基本定理列于表5.7-2。
表5.7-2 z变换的基本定理
(4)z反变换
由X(z)求x*(t)或x(kT)称为z反变换。z反变换有下面三种方法:
A.幂级数展开法
如果X(z)是真有理函数或严格真有理函数,则可利用长除法把它展成z-1的幂级数,即

根据X(z)的定义,z-k的系数Ck就是x(kT)。这种方法适用于简单函数,但难以求得答案的封闭形式。
例1 对于

则x(kT)为:x(0)=0,x(T)=1,x(2T)=3,x(3T)=7,x(4T)=15,…。
B.部分分式法
当X(z)为z的有理函数,且其分母多项式能分解因式求出极点时,可以利用部分分式法把X(z)变成分式和的形式,然后再根据z变换表求出x*(t)或x(kT)。
说明:鉴于z变换表中的z函数的分子通常都含有z因子,因此,首先把X(z)/z展开成部分分式,然后将所得的结果,各项再乘以z,就得到X(z)的分式和的形式。当X(z)/z只含有单极点时,则有

式中,zi是X(z)/z的极点,Ai是相应于zi的留数,即

例2 对于

因为

则有

将上式去查表5.7-1得
x(kT)=2k-1
于是,x(0)=0,x(T)=1,x(2T)=3,x(3T)=7,…
C.留数法
如果已求出X(z)的极点zi,则可应用留数计算x(kT),即

式中Res[·]表示函数在极点上的留数,zi是X(z)·zk-1的极点,i是极点数,k=0,1,2,…。应注意:当k=0时,X(z)zk-1=X(z)z-1,在原点可能有一个极点。若有此极点,则X(z)zk-1在原点处的留数也应计算,并且把这点的留数x(kT)乘以δ(k),此处δ(k)定义为

例3 对于

则有

根据式(5.7-13)则得

于是,x(0)=0,x(T)=1,x(2T)=3,x(3T)=7,x(4T)=15,…