电液伺服阀的传递函数
出处:按学科分类—工业技术 北京理工大学出版社《新编液压工程手册上册》第1176页(2898字)
(1)概述
伺服阀传递函数是伺服阀动态特性的近似线性解析表达式,它用于系统的线性化动态分析,特别是系统稳定性的线性分析。
伺服阀的实际动态特性与供油压力、输入信号幅值、油温、环境温度、负载条件等许多因素有关。从自动控制的观点来看,伺服阀是一个高度复杂的装置,具有高价的非线性动态特性。因此,用一阶,二阶,甚至三阶传递函数描述伺服阀的动态特性,也仅仅是对伺服阀实际动态特性的一个近似等效。
在大多数电液伺服阀系统中,伺服阀的动态响应往往高于系统负载的动态响应。因此,在分析系统动态特性时,只需要知道在一个适当的低频段内的伺服阀动态特性,也就是说,伺服阀传递函数只需要在某个低频区段内与实际伺服阀动态特性有较精确的近似等效关系,就是足以满足系统设计和分析的需要。
为简化分析,并考虑到具有较好的等效精度,从实用角度出发,一般伺服阀采用二阶振荡环节形式的传递函数。若伺服阀在某些系统应用中,它的动态响应大大高于系统负载的响应,例如10倍以上,这时,可以把伺服阀看作一阶惯性环节,甚至看作一个比例环节。
上述伺服阀等效传递函数中的系数,最好是根据实际使用条件进行伺服阀动态特性试验,然后通过计算机辅助的曲线拟合技术确定。
但在系统设计阶段,系统设计者手中尚无现成的伺服阀,或者需要通过系统分析确定所需的伺服阀动态特性,这时,可以根据伺服阀样本中给出的幅频宽和相频宽等方面的指标数据,并参照以下所述的内容估计伺服阀的传递函数。
(2)电液流量伺服阀传递函数
对于通用型流量伺服阀,一阶近似传递函数可以由下式估计
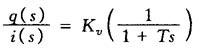
式中 q(s)——输出流量(cm3/s);
i(s)——输入电流(mA);
s——拉氏算子(1/s);
Kv——负载压降为零处的伺服阀静态流量增益[(cm3/s)/mA],Kv=qn/In;
qn——额定流量(cm3/s);
In——额定电流(mA);
T——伺服阀时间常数(s),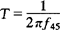 ;
;
f45——对应于相位滞后45°的频率(Hz)。
二阶近似传递函数可以由下式估计
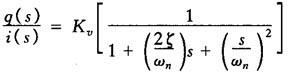
式中 ωn——伺服阀固有角频率(rad/s),ωn=2πfn;
fn——对应于相位滞后90°的频率(Hz);
ζ——阻尼系数,无因次量;取决于伺服阀类型及规格,一般为0.5~1。
(3)电液压力伺服阀传递函数
对于四通双向正增益的通用型压力伺服阀具有的压力一流量特性,当负载腔锁闭时,其二阶近似传递函数可由下式估计
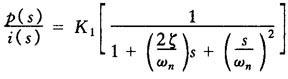
式中 p(s)——输出压力(MPa);
i(s)——输入电流(mA);
K1——压力伺服静态流量增益(MPa/。mA);
ωn——伺服阀固有角频率(rad/s),ωn=2πfn;
fn——对应于相位滞后90°的频率(Hz),典型参考值:fn=200Hz;
ζ——阻尼系数,无因次量;取决于伺服阀类型及规格,典型值为:ζ=0.3~0.5。
当压力伺服阀提供负载流量时,其传递函数为p(s)=[K1i(s)-K2(1+Ts)q(s)]

式中 K1——负载腔锁闭时的压力增益(MPa/mA);
K2——输出压力为零处的流量—压力系数,或称负载压力下降系数[MPa/(cm3/s)],典型值:0.14~0.35MPa/(cm3/s);
T——与负载有效流量及油液可压缩性流量等有关的时间常数,或称压力下降的时间常数(s),典型值为:T=0.016s;
ωn——伺服阀固有角频率(rad/s),ωn=2πfn;
fn——固有频率(Hz),典型值为:fn=200Hz;
ζ——阻尼系数,无因次量,典型值为:ζ=0.5。
(4)动压反馈流量伺服阀传递函数
对于图20.4-11所示的动压反馈流量伺服阀,其等效传递函数可由下式估计
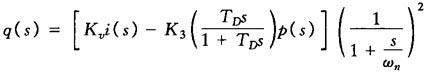
式中 q(s)——输出流量(cm3/s);
p(s)——负载压力(MPa);
i(s)——输入电流(mA);
s——拉氏算子(1/s);
Kv——伺服阀静态流量增益[(cm3/s)/mA];
K3——压力—流量系数[(cm3/s)MPa];
TD——动压反馈网络时间常数(s),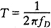
fD——动压反馈网络转折频率(Hz);
ωn——过阻尼的伺服阀固有角频率(rad/s),ωn=2πfn;
fn——固有频率(Hz),对带动压反馈网络的伺服阀进行动态测试时,对应相位滞后90°的频率。