分析法设计平面连杆机构

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1918页（18261字）

采用分析法设计平面连杆机构，需先建立机构参数与运动条件之间的关系式，然后根据关系式采用不同的数学方法(如向量、复数、矩阵、旋量等)，按一定的准则，求解满足给定运动条件的机构未知参数。这里将介绍位移矩阵设计法和复数封闭环设计法。

3．2．1 刚体导引机构的设计

1．位移矩阵设计法

如图5．4-19所示，当平而刚体S由位置S₁运动到位置S_j，若已知基点P的位置坐标(p_jx、P_jy)及标线PQ的对应位置角θ_j，则根据线性代数待求点Q的位置可表示为：

图5．4-19 平面位移矩阵

称为平面运动刚体的位移矩阵，而θ_1j=θ_j－θ₁，(j=2，3，…，N)，N为给定的平面运动刚体位置数。规定：θ角逆时针方向转动为正，反之为负。

由于平面连杆机构的运动副只有转动副和移动副两种形式，因而这时导引杆也只有R-R杆和P-R杆两种形式。R-R导引杆如图5．4-20所示，用平面R-R导引杆使连杆占据给定的位置PjQj(j=1，2，……，n)时，动铰链中心A₁应为圆点，而定铰链中心A₀应为相应的圆心，各相关点A_j(j=1，2，……，n)在以A₀A₁为半径的圆周上。由此可得平面R-R导引杆的位移约束方程——定长方程：

图5．4-20 R-R导引杆

当给定连杆的各位置，即已知P_j、θ_j(j=1，2，……，n)时，〔D_1j〕为已知，其中各元素可按式(5．4-7)中各对应元素求得。将式(5．4-9)代入式(5．4-8)，可得仅包含圆点和圆心未知坐标a_1x、a_1y、和a_ox、a_oy的参数方程，亦即平面R-R导引杆的设计方程。该方程为二阶非线性方程。

P-R导引杆如图5．4-21所示，用平面P-R导引杆使连杆占据给定的位置P_jQ_j(j=1，2，……，n)时，动铰链中心B的相关点B₁、B₂、……、B_n应在一直线上，转动副Bo演化为移动副。由此可得P-R导引杆的位移约束方程——定斜率方程：

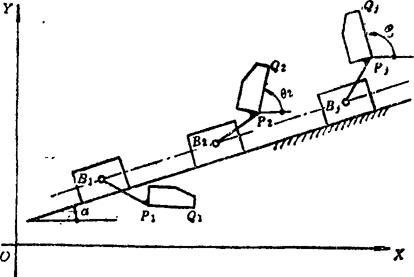
图5．4-21 P-R导引杆

同理，按式(5．4-6)，有：

式中位移矩阵〔D₁j〕仍按式(5．4-7)计算。将式(5．4－12)代入式(5．4-11)，可得仅包含坐标b_1x、b_1y的设计方程，这是对未知量b_1x、b_1y的二阶非线性方程。

若给定连杆三个位置，为R-R导引杆时，式(5．4-8)和(5．4-9)的j=2、3，算出〔D12〕、〔D₁₃〕，并将式(5．4-9)代入式(5．4-8)后，可得两个设计方程：

式中有四个未知数a_1x、a_1y、a_ox、a_oy，而方程只有两个，故求解时可任选两个未知量。由此可见，给定连杆三个位置时，可有无穷多解。

设计时，通常选定导引杆的定铰链坐标a_ox、a_oy，而由式(5．4－13)求解动铰链在第一个位置的坐标a_1x、a_1y。将式(5．4-13)对a_1x、a_1y展开并化简后，可得一组两个线性方程式：

用克莱姆法则可方便地从线性方程组(5．4-14)中解出未知量a1x和a1y。

在给定连杆三个位置，且为P-R导引杆时。式(5．4-11)的j=3，只有一个约束方程。但式(5．4-12)的j=2、3，可求出b_2x、b_2y、b_3x、b_3，与b_1x、b_1y的关系式。将其代入式(5．4-11)后可得设计方程： (5．4-15)

其中d_jkj是位移矩阵〔D_1j〕中的各元素。

式(5．4-15)是圆的一般方程式，它表示满足连杆的三个给定位置时，导引滑块铰链点B可在该圆上任取。导引滑块铰链点B1的位置分布圆，称为滑块轨迹圆。将式(5．4-15)改写成圆的标准形式

于是，滑块轨迹圆的圆心坐标c_ox、c_oy和圆半径R分别为

综上所述，在给定连杆三个位置时，可得无数个能满足给定位置要求的导引滑块的解。设计时，可根据其它条件，从中选取一个适当的解。

例5．4-1设计一曲柄滑块机构^(21〕，要求能导引连杆平面通过以下三个位置：

P₁(1．0，1．0)

P₂(2．0，0) θ₁₂=30°

P₃(3．0，2．0) θ₁₉=60°

设计的内容和步骤如下：

①导引滑块的设计

求滑块铰链中心B₁的轨迹圆：由式(5．4-7)，得：

将各元素值代入式(5．4-16)，求得各系数

E=0．134 F=0．5 A=0．134

B=－1．036 C=1．866 D=5．634

将它们代入式(5．4－17)，得轨迹圆方程(b_1x－3．8657)²+(b_1y－6．9627)²=(4．6236)²

于是，滑块轨迹圆的圆心坐标以及半径R为：c_ox=3．8657、c_oy=6．9627，R=4．6236。

选定滑块铰链中心B₁的位置坐标b_1x、b_1y：设B₁点取在轨迹圆与Y轴的交点，则b_1x=0，代入轨迹圆方程，得

(b_1y－6．9627)²=(2．5365)²

解上式，得b_1y=4．4262或b_1y=9．4992。现选取B₁=(0，4．4262)。

求滑块导路的倾角a：滑块铰链点的第二、第三个位置B₂、B₃可按式(5．4-12)求得

(b_2xb_2y1)^T=〔D₁₂〕(b_1xb_1y1)^T

=〔D₁₂〕(04．42621)^T

=(－0．57912．46711)^T(b_3xb_3y1)^T=〔D13〕(b_1xb_1y1)^T

=〔D₁₃〕(04．42621)^T

=(－0．46712．84711)^T

代入式(5．4-10)，得

即 a=tg^－13．3832=73．53°。

② 导引曲柄的设计

求动铰链A₁的位置坐标a_1x、a_1y：取曲柄的固定铰链中心A_o=(0，－2．4)，代入式(5．4-14)得方程组

解此线性方程组可得a_1x=－7．8630，a_1y=－6．9787。

求动铰链点A的另两个位置A₂、A₃：

(a_2xa_2y1)^T=〔D₁₂〕(a_1xa_1y1)^T

=〔D₁₂〕(－7．8630－6．97871)^T

=(－1．6860－11．34111)^T

(a_3xa_3y1)^T=〔D₁₃〕(a_1xa_1y1)^T

=〔D₁₃〕(－7．8630－6．9781)^T

=(5．4781－9．66471)^T

计算机构各构件的相对尺寸：

由于，故有曲柄存在，设计所得的为曲柄滑块机构，其运动简图如图5．4-22所示。

图5．4-22 曲柄滑块机构设计

四、五个位置设计：给定连杆四个位置，设计R-R导引杆时，式(5．4-8)和(5．4-9)中的j=2，3、4，于是可得方程组：

式中 (a_jxa_jy1)^T=〔D_1j〕(a_1xa_1y1)^Tj=2、3、4位移矩阵〔D_1j〕为已知，故方程组(5．4-19)包含未知量a_ox、a_oy、a_1x、a_1y。从中任选一个，如a_ox，可求解其余三个未知量。此时比三个位置时多一个未知量，无法展开成式(5．4-14)形式的线性方程组，从而得到一组含三个未知量的二阶非线性方程。由于任选的一个参数，其值可任意假定，故通过解非线性方程组，可得到一系列动铰链点(圆点)和定铰链点(圆心)，因而得到相应的一对圆点曲线和圆心曲线。如果给定连杆五个位置，这时将求解一组四个式(5．4-19)形式的非线性方程。为求解方便，通常采用计算两组四个位置的方法，即求1、2、3、4位置和1、2、3、5位置圆点曲线(或圆心曲线)的交点，以得到所需的布氏点(或布氏中心)。当然，也可能得不到交点，即无解。

对于P-R导引杆的四位置设计，由于需求解的是两个式(5．4-15)形式的二阶非线性方程(滑块轨迹圆方程)，故其迭代解法与R-R导引杆设计类似，只是所求的解将位于两个滑块轨迹圆(如1、2、3位置和1、2、4位置)的交点。

例5．4-2设计一铰链四杆机构〔21〕，能导引连杆平面通过以下四个给定位置：

P₁=(1．5，0．5)

F₂=(2．5，0．0)θ₁₂=0°

P₃=(3．5，1．0)θ₁₃=30°

P₄=(2．3，1．5)θ₁₄=35°

解：采用牛顿-莱夫森迭代法求解式(5．4－19)的三个非线性方程组。其初始值选取：

a_ox=0．0，a_oy=0．0。a_1x=1．6，a_1y=4．6通过不断给a_ox值以增量△a_ox，于是，可算得一系列的Ao(a_ox，a_oy)、A₁(a_1x，a_1y)坐标，如图5．4-23所示。所有的A_o(a_ox，a_oy)点形成一条圆心曲线m₁₂₃₄，所有第一位置的A₁(a_1x，a_1y)点形成一条对应的圆点曲线(图中仅表示了取a_ox=0～1．8时的一段曲线)。在m₁₂₃₄上取A₀和B₀两点作为机构的固定铰链中心，在上取与A₀、B₀对应的两点A₁、B₁为连杆的动铰链中心，于是得到铰链四杆机构A₀A₁B₁B₀，它能导引连杆B₁A₁P₁通过给定的四个位置。

图5．4-23 给定连杆四个位置设计

2．复数封闭环设计法

图5．4-24所示为一平面铰链四杆机构在位置1(实线)和任一位置j(虚线，j=2，3，……)的两个不同位置。图中各杆均以向量表示，整个四杆机构可以看作是两个双向量(即标准形)组成Z₁-Z₂和Z₃－Z₄。其中Z₂和Z₄同属连杆平面。在设计中，这四个向量确定了，圆点A、B和圆心点O_A、O_B即随之确定。另两向量Z₅和Z₆也可由下式求得

图5．4-24 标准形方程

Z₅=Z₂－Z₄ (5．4-20)

Z₆=Z₁+Z₅－Z₃ (5．4-21)

对于双向量来说，其位置1和任一位置j均构成闭环O_AA_jP_jOP₁AO_A，可写出闭环复数方程

Z_1e^iφ_j+Z₂^eia_jR－_j+R₁-Z₂-Z₁=0

(5．4-22)

或Z₁(e^iφ_j－1)+Z₂(^eia_j－1)=δ_j (5．4-23)

式中，δj表示连杆平面上点P从P₁(位置1)到P_j(位置j)的位移向量。若P₁和P_j的位置分别以向量R₁和R_j表示，则

δj=R_j－R₁

式中，φ_j和a_j分别表示向量Z₁和Z₂从位置1到位置j的转角。

式(5．4-23)称为标准形方程，是一复数方程(或向量方程)，分离实部和虚部，可得两个实数方程，能解两个未知实数。另一组双向量Z₃-Z₄，也可得到类似的标准形方程。

由图5．4-24可知，当给定连杆平面一点(例如P)的位置及其方位角时，则该平面的位置即完全确定。位置设计中给定位置的最大可能数见表5．4-9．表中列有给定位置数、实数方程数、未知实量数、任选实量数和解的可能数之间的关系。

表5．4-9 位置设计给定位置的最大可能数

对于二位置设计(j=2)，由式(5．4-23)得：

Z₁(_e^jφ₂－1)+Z₂(e^°a₂－1)==δ₂

(5．4-24)

式中δ₂和a₂已知。任选三个未知实量，如Z₂的二个分量和φ₂，则可由下式求向量Z₁

对于三位置设计(j=2、3)，由式(5．4-23)得：

式中δ₂、δ₃和a₂、a₃已知，还必须任选两个未知实量才能有解，故选Z₁和φ₃，从而使式(5．4-26)成为Z₁和Z₂的线性方程组，可利用克莱姆法则求解得2

对于四位置设计(i=2、3、4)，由式(5．4-23)得：

式中δ₂、δ_：、δ₄和a₂、a₃、a₄为已知量。由表5．4-9可知，任选一未知实量，其余未知量可由方程组(5．4-29)解出。为求解方便，试将方程组(5．4-29)视为Z₁和Z₂的线性非齐次方程组，写成矩阵形式，得：

如式(5．4-30)有解，则有

式(5．4-31)称为方程组(5．4-29)的相容条件，将此行列式按第一列展开得：

△₂^eiφ3+△₃^eiφ₈+△₄^eiφ₄+△₁=0 (5．4-32)

式中 △₁=－△₂－△₃－△₄ (5．4-33)

式(5．4-32)称为相容方程式。△₁、△₂、△₃和△₄均为已知量，凡满足此方程的一组解φ₂、φ₂和φ₄，将使方程组(5．5-29)相容，可使Z₁和Z₂，有解。此外，由式(5．4-32)和(5．4-33)可知，如将向量△₁、△₂、△₃和△₄视为某一假想的四杆机构的四个杆，称为相容四杆机构，如图5．4-25所示，令A1作机架，△₂作主动件，△₃作连杆，△₄作从动件，则上述二式恰好是该相容四杆机构的闭环复数方程．式(5．4-33)表示其初始位置(实线)，式(5．4-32)则表示其主动件△₂转过φ₂角之后的位置(e^iφj为转动算子)。因此，φ₃和φ₄即是其连杆△₃和从动件△₄由初始位置转过的角度。由图可知，对应于任一选定的φ2值，△₂^eiφ₂位置一定，△=△₁+△^2eiφ2也一定，但△3^eeiφ8和 △4^eiφ4却有两种可能的位置，分别用虚线和点划线表示，而φ₃和φ₄也相应有两组可能的解，可由下列关系式求得：

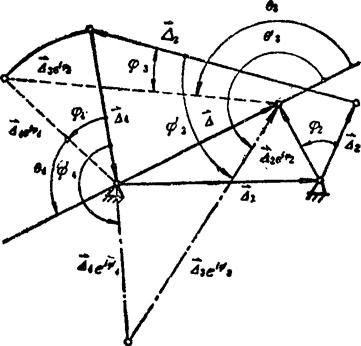
图5．4-25 相容四杆机构

将φ₃、φ₄和、两组解分别代入式(5．4-29)中任意二式，按克莱姆法则即可求得两组Z₁和Z₂值，然后由下列二式可得两组圆点4和圆心点O_A的位置向量(参见图5．4-24)；

k1=R₁－Z_： (5．4-43)

m=k₁－Z₁ (5．4-44)

式中：k₁=OA，m=OO_A(图5．4-24中未标出k和m)。故此，当选定一系列φ₂值时，则可求得一系列圆点和圆心点，将这些点描成曲线，即为圆点曲线和圆心曲线。由式(5．4-43)求得圆点，位于位置1的运动平面上(因此k₁取下标1)，而由式(5．4-44)求得的圆心点，则位于固定平面上，两者一一对应。角φ₂的取值范围完全由相容四杆机构中主动件△₂的可能转动范围决定。若△₂为曲柄，则φ₂=0～2π；△₂为摇杆，则φ₂只能在小于2π的某一范围内取值。这两种情况可按四杆机构有曲柄的条件加以判别。

若给定运动平面五个位置(j=2、3、4、5)时，由式(5．4-23)得：

由表5．4-9可知，此时未知实量数等于实数方程组。故全部未知量均由方程组解出。同四位置设计一样，将方程组(5．4-45)视为Z₁和Z₂的线性非齐次方程组，如果有解，则有：

此类问题的解(即圆点和圆心点)可能得4个、2个解或无解。

例5．4-3 某装配线需设计一四杆机构，将部件从一条传送带转运到另一条传送带上，如图5．4-26a)所示^〔20、43〕。已知部件三个必经的位置：装取、卸放和某中间位置，即δ₂=－6+11i，δ₃=－17+13i，a2=22°，a3=68°。

图5．4-26 三位置设计

这是给定运动平面三位置的位置设计，其设计方法和步骤如下：

求四杆机构左侧双向量Z₁－2₂(参见图5．4-24)：设φ₂=90°，φ₂=198°，由式(5．4-27)和(5．4-28)得

求右侧双向量Z₃－Z_4；设ψ₂=40°，ψ₃=73°。由式(5．4-27)和(5．4-28)并以ψ取代φ得

求连杆和机架向量Z₅和Z_6：由式(5．4-20)和(5．4-21)得

Z₅=Z₂－Z₄=16．0313-9．4215i=18．5948－30．443°

Z₆=Z₁+Z₆－Z₂=3．4118-8．2796i

=8．9550－67．605°

综合所得四杆机构的运动简图及其三个位置如图5．4-26b)所示。

例5．4-4 如图5．4-27所示，^〔20、42〕需设计一四杆机构将过滤器毛坯从料斗转置于芯轴上。毛坯需经过的四个位置规定如下：

图5．4-27 毛坯需经过的四个位置

这是一四位置设计。根据已知量δ₂=3+5i、δ₃=27+22i、δ₄=35+24i、a₂=5°、a₃=90°和a₄=117°，由式(5．4-29)～(5．4-44)可求得圆点曲线K和圆心曲线M，(如图5．4-28a)所示。在圆心曲线M上任选两点作为O_A和O_B，再按圆点与圆心点一一对应的关系，在圆点曲线K上求得相应的圆点作为A₁和B₁。O_BA₁B₁O_B即为所求的四杆机构，如图5．4-28b)所示，其连架杆O_AA₁主动，可按规定顺序引导连杆平面经过各规定位置，且传动角合适。

图5．4-28 四位置设计

3．2．2 传动机构的设计

1．位移矩阵设计法

传动机构的设计即是实现给定函数机构的设计，它按两连架杆给定的若干组对应位置确定机构的设计参数。对该类型机构的设计，通常是转化为实现刚体导引机构的设计。

实现给定函数的传动机构，由于两连架杆的位置关系仅与各杆的相对长度有关，故进行设计时一般选取机架的长度A₀B₀=1。图5．4-29所示铰链四杆机构，即取固定铰链中心A0为坐标原点，另一固定铰链中心B0的坐标为(1，0)。若将机构的第j个位置B_jB₀A₀A_j看成一刚体，并绕B_o点转过(－ψ_1j)=－(ψ_j－ψ₁)，使从动连架杆B₀B_j与B_oB₁重合，则机构将由位置B_jB₀A₀A_j转到新的位置，即原从动连架杆转化为“机架”，原机架和连杆转化为“连架杆”，而原主动连架杆转化为“连杆”。于是，通过转换机架法，就把按给定位置φ_j、ψ_j(j=1，2，……，n)设计实现函数机构的问题，转化为按给定的“连杆n的位置A₀A₁、(j=1，2，……，n)设计刚体导引机构的问题。因此，利用式(5．4-6)可写出的位置方程式

图5．4-29 实现给定函数的传动机构

称为平面相对位移矩阵。

对于图5．4-30所示的曲柄滑块机构，可取A₀为坐标原点。其转换机架的方法与前述相同，只是应将第二个运动看成是刚化了的第j个位置A₀A_jB_j沿导槽a的方向移过(－s_1j)。于是有，

图5．4-30 曲柄滑块机构

应该注意的是，式(5．4-49)和(5．4-50)的相对位移矩阵〔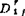_j〕，是按图5．4-29和5．4-30的坐标系取法而导出的，因此在引用计算式时，必须满足规定的坐标取法。

图5．4-29所示的平面连杆机构，经转化机架后，原连杆均变成平面R-R导引杆，因此可按式(5．4-14)的线性设计方程组求解未知参数a_1x和a_1y。所不同的是，式(5．4-14)中的固定铰链中心坐标A₀(a_0x，a_oy)应以转化后的新固定铰链中心B₁(b_1x，b_1y)代替，连杆转角θ_1j以新连杆的转角φ_1j－ψ_1j代替，位移矩阵〔D_1j〕的各元素应以相对位移矩阵〔j〕的相应元素代替。于是，式(5．4-14)可写成如下形式：

由于式中的b1x、b1y可任选，故可得到一系列的解。

由给定的函数关系选四个精确点算出铰链四杆机构主、从连架杆的位置角φ_j、ψ_j(j=1，2，3，4)后，可根据假想导引杆AB的定长条件建立三个设计方程：

式中。显然，这是一组三个含有四个未知量(a_1x，a_1y，b_1x，b_1y)的非线性设计方程，其中有一未知量可预先选定。用数值迭代法求解时，若使预先选定的未知量不断增值，可得到一系列解，用以画出相对圆点曲线和相对圆心曲线。从曲线上适当选取两组对应的圆点、圆心点，即可得到所需的机构。

例5．4-5 设计一铰链四杆机构，能近似实现给定的函数y=1ogx，x的变化区间为1≤x≤2，主、从动连架杆的最大摆角分别为60°和90°。^(21〕

首先，按三个精确点计算对应的φ_j、ψ_j角如下：

① 按已知条件x₀=1、x_l=2，得y₀=1ogx₀=和y_j=logxj=0．301。

② 计算比例系数μ_φ和μ_v，得

③ 按戚贝谢夫精确点分布式计算精确点的x_j、y_j值：

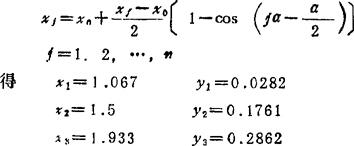
④ 按下式计算φ_j、ψ_j角：

当取φ₀=86°、ψ₀=23．5°时，得

φ₁=90．02° ψ₁=31．93°

φ₂=116° ψ₂=76．15°

φ₃=141．98° ψ₃=109．07°

⑤ 按下式计算相对于第一个位置的φ_1j、ψ_1j角：

得 φ₁₃=25．98° ψ₁₂=44．22°

φ₁₃=51．96° ψ₁₃=77．14°

第二步，计算相对位移矩阵〔〕：由式(5．4-49)，得

第三步，由式(5．4-51)建立设计方程组：当取b_1x=1．348，b_1y=0．217时，得

用克莱姆法则解此线性方程组，得

a_1x=0．018 a_1y=0．7435

第四步，计算各杆的长度：因已假定固定铰链的坐标为A_o(a_0x，_aoy)=(0，0)，B₀(b_ox，b_oy)=(1．0)，故可得各杆的相对长度为

根据实际条件选取机架长度l_A0B0=100mm，则其余各杆长度为

l_AoA=100×A₀A=74．37mm

l_AB=100×AB=143．04mm

l_B0B=100×B_oB=41．01mm

所得机构的简图如图5．4-31所示。

图5．4-31 三个精确点设计

例5．4-6 在上例再增加一精确点x₁=1，y₁=0，试设计近似实现给定函数y=1ogx(1≤x≤2)的铰链四杆机构。^〔21〕

四个精确点为：

x₁=1 y₁=0

x₂=1．067 y₂=0．0282

x₃=1．50 y₂=0．1761

x₄=1．933 y₄=0．2862

对应的转角为：

φ₁=φ₀+0° ψ₁=ψ₀+0°

φ₂=φ₀+4．02° ψ₂=ψ₀+8．43°

φ₃=φ₀+30° ψ₃=ψ_o+52．65°

φ₄=φ_o+55．98° ψ₄=ψ_o+85．57°

相对于第一个位置的转角为：

φ₁₂=4．02° ψ₁₂=8．43

φ₁₃=30° ψ₁₃=52．65°

φ₁₄=55．98° ψ₁₄=85．57°

利用牛顿-莱夫森法解非线性方程组的计算机程序进行迭代求解，当预先选定未知量b12=1．35。并不断给b1x以增量0．2时，可得一系列解如下：

取其中第一组数值作为机构的解，则可画出如图5．4-32所示机构简图。其中各杆的相对长度为：

图5．4-32 四个精确点设计

2 复数封闭环设计法

如图5．4-33所示封闭环θ_AA_jB_jO_BBAO_A可得Z₁(e^iφj－1)+Z₅(e^iaj－1)－Z₃(e^iφj－1)=0

(5．4-53)

图5．4-33 实现给定函数的传动机构设计这是三向量复数方程，与标准形方程不同。对实现给定函数的传动机构设计来说，φ_j和ψ_j为已知量，其余都是未知量。根据导引机构设计中分析给定位置的最大可能数的方法，由式(5．4-53)分析实现给定函数的传动机构设计中给定连架杆对应位置的最大可能数见表5．4-10。由表可知，实现给定函数的传动机构设计中给定对应位置的最大可能数为七。但实际上，该数目是五而不是七。因为实现给定函数的传动机构设计只需二连架杆的转角再现给定的函数关系，与机构的构件尺寸的绝对大小和整个机构的配置方位无关，形状相似而大小和方位不同的两个铰连四杆机构，其连架杆的转角关系完全相同。因此，可随意选定式(5．4-53)中三个向量之一的大小和方向，而不影响设计的结果。如选定z₃，则式(5．4-53)就成为标准形方程：

表5．4-10 实现给定函数的传动机构设计给定连架杆对应位量的最大可能数

(5．4-54)

据此分析给定对应位置的最大可能数与表5．4-9相同，即为五。这样，实现给定函数的传动机构设计问题的解法，就和导引机构的设计完全一致了。其唯一的区别是，这里的已知量是δ_j和φ_j，而导引机构的设计则是δ_j和a_j。

值得注意的是，实现给定函数的传动设计只需一个双向量，即图5．4-33中的Z₁－Z₅。因此，在给定五组连架杆对应位置时，同五位置设计一样，可得4个、2个或零个双向量组，最多也只能得到4个、2个或零个四杆机构。但其中总有一个解没有实际意义，即|Z₁|=0、Z₅=Z₃，因而a_j=ψ_j。可见，五精确点的设计，最多只能得到三个不同的四杆机构。

3．2．3 导向机构的设计

1．位移矩阵设计法

图5．4-34所示为铰链四杆机构A₀A₁B₁B₀。设连杆AB上一点P在坐标系xoy中，沿平面轨迹的一系列给定的有序点P₁、Pj(j=2、3、4……)运动。由于P_j点的坐标(P_jx、p_jy)为已知，故需确定四个铰链中心A₀、A₁、B₀、B₁的坐标。为此，可列出两连架杆的约束方程：

图5．4-34 给定轨迹上一系列有序点的设计

为了求解连杆上点A_j(或B_j)的位置，利用式(5．4-6)得

其中〔D_1j〕见式(5．4-7)，即

式中θ_1j为连杆的相对转角，此时为未知量；p_1x、p_1y，p_jx、P_jy为参考点的坐标，这时即为轨迹上给定的设计点的已知坐标值。将式(5．4-56)代入式(5．4-55)，经整理后得非线性设计方程组：

其中有八个未知的结构参数(a_ox，a_oy，a_1x，a_1y，b_ox，b_oy，b_1x，b_1y)和j－1个未知的运动参数(θ₁₂，θ₁₃，……，θ_1j)，即共有8+(j－1)个未知参数，而设计方程的数目为2(j－1)。由8+(j－1)≥2(j－1)可得j≤9，即最多可实现轨迹上九个给定的设计点。铰链四杆机构轨迹设计时给定的设计点数目与可选定的参数数目的关系见表5．4-11。由表可见，当j≤5时，可预先选定四个以上参数．若将所有的连杆相对转角θ_jj均预先选定，则此时轨迹机构的设计转化成刚体导引机构的设计，从而可对两个连架杆分别独立求解其铰链中心的坐标。

表5．4-11 设计点数自与可预选的参数数目的关系

如图5．4-34所示，除了要求连杆上一点P在坐标系XOY中沿平面轨迹上一系列给定的有序点P₁、P_j(j=2，3，4，……)运动之外，同时，曲柄A_oA_j与P_j点对应时的转角φ_1j还需满足给定的值。这种情况相当于前述的给定轨迹上一系列有序点的设计再增加一个定长约束条件

则Aj点的位置方程为：

将式(5．4-60)代入(5．4-59)可得j－1个附加的设计方程，且再与式(5．4-58)联立求解，将使所得的机构即满足给定的轨迹设计点，又满足给定的曲柄对应转角φ1j。

用上述方法求解机构时，机构参数仍为8+(j－1)个，但设计方程从2(j－1)个增加到3(j－1)≤8+(j－1)，可得j≤5，即最多可给定轨迹上五个设计点。如取j=5，不仅需求解12个非线性设计方程，而且其中还包括未知量数目较多的方程式(5．4-58)。为此，可采用另一种简便的方法，即先建立约束方程

然后将式中的a_jx、a_jy用式(5．4-60)代入，经整理后得设计方程：

非线性方程组式(5．4-62)仅含四个未知参数a_0x、a_oy、a_1x、a_1y。用数值迭代法解得这四个参数后，再用式(5．4-60)计算出a_jx、a_jy(j=2，3，4，5)，并由

计算出连杆的位置角θ_j和相对转角θ_1j。最后将p_jx、P_ly、θ_1j作为已知值，按刚体导引机构的设计方法设计导向杆B_oB_，解出其铰链中心的四个坐标b_0x、b_oy、b_1x、b_1y。

图5．4-35所示为曲柄滑块机构A₀A₁B₁。设连杆AB上一点P在坐标系XOY中沿平面轨迹上一系列给定的有序点P₁、P_j(j=2，3，4，……)运动。由于P_j点的坐标(p_jx、P_jy)已知，故需确定三个铰链中心A_o、A₁、B1的坐标和滑块导槽的倾角a。为此，先列出两连架杆的约束方程：

图5．4-35 曲柄滑块机构

其中〔D_1j〕是以P点为参考点时连杆AB的平面位移矩阵，按式(5．4-57)计算，但此时其中的连杆相对转角θ1j是未知量。

再将式(5．4-65)代入式(5．4-64)，经整理后得非线性设计方程组：

式(5．4-66)中含七个未知结构参数(a_ox，a_oy，a_1x，a_1y，b_1x，b_1y，a)和j－1个未知运动参数(θ₁₂，θ₁₃，……，θ_1j)，即共有7+(j－1)个未知参数，而设计方程的数目仍为2(j－1)。由7+(j1)≥2(j－1)可得j≤8，即最多可实现轨迹上八个给定的设计点。j≤4时，轨迹机构的设计可转化为导引机构的设计，从而可对两个连架杆分别独立求解未知参数。

如给定轨迹上一系列有序点及其对应的曲柄转角φ_1j，由3(j－1)≤7+(j－1)可知，最多可给定轨迹上的四个设计点。这类问题同样可用类似铰链四杆机构的综合方法，按给定的设计点数目，依次分别求解连架杆A₀A₁的未知参数a_0x、a_oy、a_1x、a_1y和连架滑块B的未知参数b_1x、b_1y、a。

例5．4-7 设计一铰链四杆机构，使其连杆上某点P能依次通过平面轨迹上的七个给定设计点(其中1、2、3、7点在R=174mm的圆弧上，4、5、6点在r=100mm的同心圆弧上)。^{〔19、22、21〕}

由表5．4-11可知，当给定轨迹上七个有序点设计铰链四杆机构时，共有12个设计方程式。现共有14个设计参数，其中六个是未知的运动参数θ_1j(j=2，3，……，7)，八个未知的结构参数a_ox、a_oy、a_1x、a_1y、b_ox、b_oy、b_1x、b_1y，故可预选定两个设计参数。现选定a_ox=0，a_oy=0，亦即使A_o(a_ox，a_oy)点与坐标原点重合。

各未知设计参数的初始值选为：

a₁₁=－82．512mm，a_1y=70．711mm。

b_ox=190．4mm，b_oy=1mm。

b_1x=89．684mm，b_1y=158．199mm。

θ₁₂=0．15377rad，θ₁₃=0．38271rad，

θ₁₄=1．17461rad，θ_1s=1．0975rad，

θ₁₆=1．00356rad，θ₁₇=－0．05218rad。

采用阻尼最小二乘法解方程组(5．4-66)，经13次迭代，求得

a_1x=－95．5232mm。a_1y=80．4073mm，

b_ox=174．194mm，b_oy=18．5748mm，

b_1x=76．7907mm，b_1y=170．535mm，

θ₁₂=0．145752rad，θ₁₃=0．349826rad，

θ₁₄=1．41086rad，θ₁₅=1．32956rad。

θ₁₆=1．23331rad，θ₁₇=－0．0657764rad。

各杆的尺寸及连杆上P点位置的确定：

由各杆尺寸可知，最短杆为连架杆A₀A₁，最长杆为连杆A₁B₁，则

319．32=lA₀A₁+lA₁B₁＜lB₀B₁+lA_oB_o=355．68

故连架杆A_oA₁为曲柄。最后，作出机构运动简图，如图5．4-36所示。该机构为曲柄摇杆机构，当曲柄逆时针方向转动时，连杆上的P点将依次通过轨迹上七个给定的有序设计点。

图5．4-36 轨迹设计

2．复数封闭环设计法

按图5．4-24所示，四杆机构左右两侧双向量的标准形方程为

在轨迹设计中，仅已知连杆上P点的位置，即式(5．4-67)中δ_j是唯一的已知量，其余均为未知量。由于式中Z₂和Z₄同属连杆平面，其转角aj相同，因此由一式求得a_j后，将其代入另一式中即为已知量。为此，轨迹设计时应将两侧的标准形方程结合在一起予以讨论。

仿效导引机构设计的分析方法，按式(5．4-67)分析实现轨迹的导向机构设计给定精确点位的最大可能数见表5．4-12。由表可知，给定轨迹精确点位的最大可能数为9。当进行9个精确点的轨迹设计时，需联立求解32个超越方程式。然而，连架杆的转角φj和ψj在设计中并非必求不可。如果将其舍弃，则未知实量数可减少一半，联立方程的总数减为16个，可用开环法按二连架杆长不变建立约束方程。即使如此，求解仍然相当困难。因此，通常是减少给定的精确点位数，任选某些未知量，以简化联立方程组的求解。

表5．4-12 轨迹设计给定精确点位的最大可能数

另一种方法，是按同时给定轨迹上的精确点位P_j和相应的输入杆转角φ_j进行设计。仿前分析式(5．4-67)可知，此时给定精确点位的最大可能数与位置设计相同(也是五个)，方程组的解法也基本一致。这时，就已知量和未知量而言，双向量Z₁-Z₂的标准形方程与函数设计的方程相同，而双向量Z₃－Z₄的标准形方程则与位置设计的一样，两者的解法在本质上无差异，只是后者需待前者求得a_j之后再求。