方程的近似解

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第47页（1074字）

若方程f(x)=0，在(a，b)上的根为ξ(未知)，可用x₁，x₂，…，x_n，…表示ζ的逐次近似值。

设f(x)，f′(x)，f″(x)在〔a，b〕上连续，f(a)、f(b)＜0，且f(x)与f″(x)在〔a、b〕上不变号，则可由下述方法求得方程的近似解：

①弦位法(比例法)：

当f′(x)与f″(x)同号时，

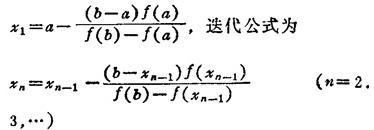
当f′(x)与f″(x)异号时，

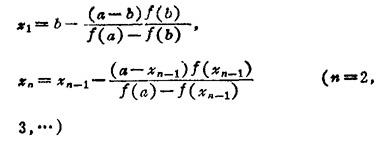
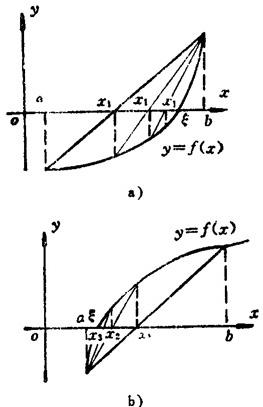
图1．1－2 弦位法

求解误差为 |x_n－ξ|≤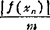。其中m为|f′(x)|在〔a，b〕上的最小值，

②切线法(牛顿法)：

当f(a)与f″(x)同号时，

x₁=a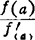－，迭代公式为

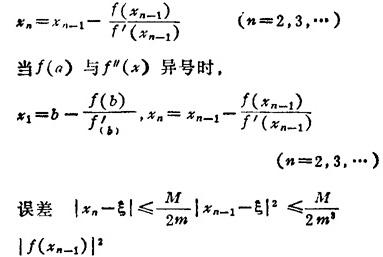
式中M、m分别为|f′(x)|在〔a、b〕上的最大值和最小值。

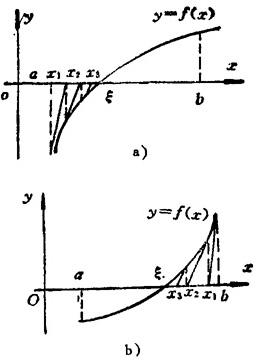
图1．1－3 切线法

③联合法(切线法与弦位法的联合使用)：当f(a)与f″(x)同号时，

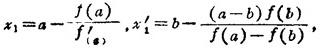
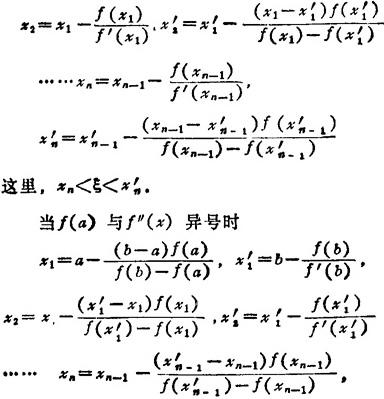
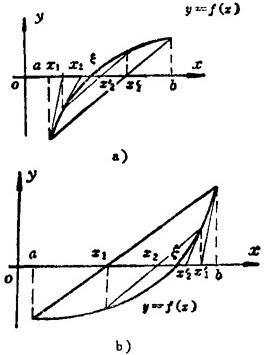
图1．1－4 联合法

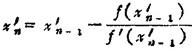
这里，x_n＜ξ＜，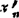

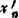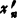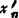误差：1x_n－ξ|≤|－x_n|或|－ξ|≤|－x_n|

④迭代法：设f(x)在〔a、b〕上连续，f(a)·f(b)＜0，且f(x)=0可以化成x=φ(x)形式，在〔a、b〕上有|φ′(x)|≤q＜1，则在〔a、b〕上任意取定一个值x0，计算

x₁=φ(x₀)，x₂=φ(x₁)，……，x_n=φ(x_n－1)则=ξ1且其误差|x_n－ξ|≤qⁿ(b－a)。