基本概念
出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第54页（3329字）
1．1．1 刚体和刚体的平衡
刚体 受力后，其形状和大小以及内部各点的相对位置都不变的物体。
刚体的平衡 在不受任何外力作用的条件下，刚体相对于惯性参考系必须保持的运动状态(如静止或等速直线平动)。工程中多数问题可把与地球固结的参考系视为惯性参考系。
1．1．2 力和力系
力 力是物体对物体的机械作用，是引起物体运动状态变化和形状改变的原因。
力系 力系是作用于同一物体上的诸力之总称。
1．1．3 力和力系的性质
力的三要素和力矢力对物体的作用效果决定于力的大小、方向和它的作用点三个要素。其中大小和方向可用一个矢量来表示，称为力矢。力的作用点连同其力矢可用带箭头的线段表示，线段的起点或终点表示力的作用点，线段的长短表示力的大小，箭头的指向表示力的方向。
作用力和反作用力 物体与物体的作用力总是成对出现的，有作用力则必有反作用力，二者等值、反向、共线，且分别作用于两个物体上，
等效力系 对刚体的作用效果相同的两个力系称为等效力系。
力系的简化与合力 用一简单的力系等效代换一复杂的力系称为力系的简化。如果能用一个力等效某一力系，则该力称为力系的合力。
两共点力的合成(平行四边形法则) 作用点相同的两力总可以合成为一合力，合力的矢量等于两力的矢量和，合力的作用点与两力的作用点相同。
二力平衡条件 力系作用于刚体上，如果刚体仍能保持其未受力时的平衡状态，则该力系称为平衡力系。平衡力系的合力为零。二力组成平衡力系的充分必要条件是：两力的大小相等，方向相反，作用线重合。
加减平衡力系原理 在任意力系中增加或减少一个平衡力系都不改变原力系对刚体的作用效果。
力的可传性作用于刚体上的力可沿其作用线改变其作用点，而不改变力对刚体的作用效果。
1．1．4 力系的特征量
力系的主矢 视力系各力矢为自由矢量，并求和所得到的合矢量称为力系的主矢，即
=Σ
(1．2－1)
力矩 可分为力对轴之矩和力对点之矩：
①力对轴之矩。力(
)对轴(z)之矩是一个代数量，它的大小等于力在垂直于轴的平面上的投影(
)的大小与其到轴和平面的交点(O)之距离(γ)的乘积，其符号按图1．2－1所示转向决定。力
为z轴之矩一般记为：
图1．2－1 力对轴之矩
②力对点之矩。力(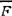
)对点(O)之矩见图1．2－2，是一个矢量，它的大小等于力对过该点且垂直于该点与力的作用线所决定的平面之轴的矩，它的方向与使力对轴之矩为正的轴向一致。显然，
力
对点O之矩可表示为
式中 r为力的作用点相对于矩心O的矢径。
图1．2－2 力对点之矩
如以矩心O为原点建立直角坐标系，则有
式中 (x，y，z)为力的作用点之坐标值；X，Y，Z分别为力
在各坐标轴上的投影。
或 
(xY－ yX)
(1．2－4)
③力对点之矩与力对轴之矩的关系：力对轴之矩等力对该轴上任一点之矩在此轴上的投影，即
(1．2－5)
式中 O点为轴z上任一点。
④合力矩定理。力系存在合力，则合力对点(轴)之矩等于力系各力(分力)对同一点(轴)之矩的矢量(代数)和。
⑤平面力系对平面上一点之矩均垂直于平面，故平面问题只需定义力对点之矩为代数量。即用力为过矩心且垂直于图面指向图外之轴的矩表示力对点(矩心)的矩，见图1．2－3。显然，力
，
对点O之矩分别为
图1．2－3 平面问题中的力对点之矩
力系的主矩 力系各力对点(或轴)之矩的矢量(或代数)和，称为力系对该点(或轴)的主矩。即力系对点O之主矩为
力系对轴z的主矩为
1．1．5 力偶和力偶矩
力偶 作用于物体上的等值、反向、不共线的一对力(
，
′)称为力偶。
力偶三要素及力偶矩矢 力偶(
，
′)对物体的作用效应取决于下列三要素：
①两力的大小和它们两作用线之距离的乘积；
②两力作用线所决定的平面(力偶的作用面)的位置；
③力偶作用面的方向(按右手螺旋法则，根据两力的相对转向，如图1．2－4约定作用面的正方
向n)。
图1．2－4 力偶的三要素
力偶的要素①和③可用一自由矢量
表示，称为力偶的力偶矩矢，或简称力偶矩。
式中 d为两力作用线的距离，称为力偶臂；
为力
偶中的力
的作用点相对于另一力
的作用点之
矢径：为力偶作用面正方向的单位矢量。
力偶的性质：
①力偶两力的主矢恒为零，力偶两力对空间任一点之主矩恒等于力偶矩矢。因此，力偶两力在任一轴上的投影之代数和恒为零，力偶两力对任一轴之矩的代数和恒等于力偶矩矢在该轴上的投影。
②力偶两力不能和一个力组成平衡力系。
③力偶两力不能合成为一个力(力偶无合力)。
④两力偶可以合成为一个合力偶，合力偶的力偶矩矢等于两个力偶矩矢的矢量和。
⑤两力偶等效的充要条件是两力偶的力偶矩矢量相等。因此，通常不画出力偶的二力，只画出力偶矩矢
，或在其作用面内画一有向弧线表示，如图1．2－5所示。
图1．2－5 力偶的图示符号