杆件的强度和刚度计算公式

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第109页（3081字）

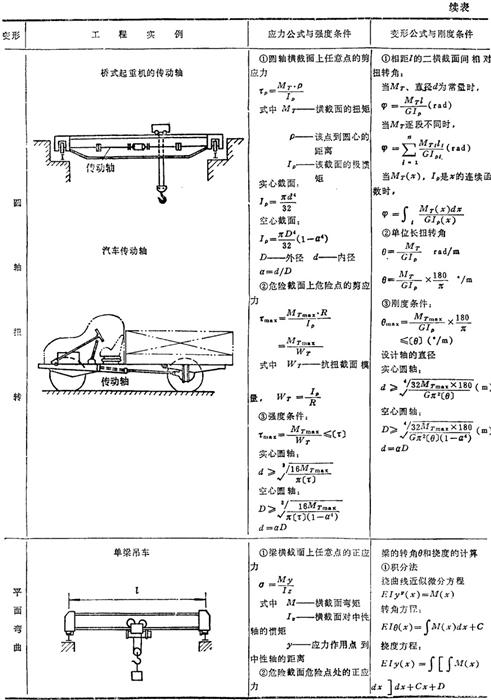
1．2．1 基本变形杆件的强度和刚度计算公式

杆件在外力作用下产生的基本变形有四种：轴向拉伸或压缩、剪切、扭转和弯曲。杆件在基本变形时的强度、刚度计算公式见表1．3－8。

表1．3－8 基本变形杆件的强度、刚度计算公式

这里需要说明的有以下几点：

①非圆截面杆扭转的强度、刚度计算不可采用表1．3－8中圆轴扭转公式。矩形截面杆扭转时的剪应力分布如图1．3－13所示，最大剪应力发生在横截面长边中点，其值为

图1．3－13 矩形截面杆横截面扭转剪应力分布

式中系数a、β与截面的长短边之比有关，见表1．3－9。

表1．3－9 矩形截面杆扭转时的系数a、β

强度条件。τ_max≤〔τ〕

刚度条件：θ_max＜〔θ〕

②一般情况下，梁的强度是以弯曲正应力为强度的控制因素，只需用正应力强度条件

进行强度计算。

当材料抗拉、抗压性能不同时，梁的强度要分别校核，即

σ_Tmax≤〔σ_T〕

σ_cmax≤〔σ_c〕

式中 σ_T、σ_c分别为拉应力和压应力。

对于诸如短梁(l／h＜5)、木梁、载荷靠近支座的情况，或工字形等薄壁组合截面梁，则除了进行弯曲正应力强度计算外，还需由剪应力强度条件

进行强度校核。

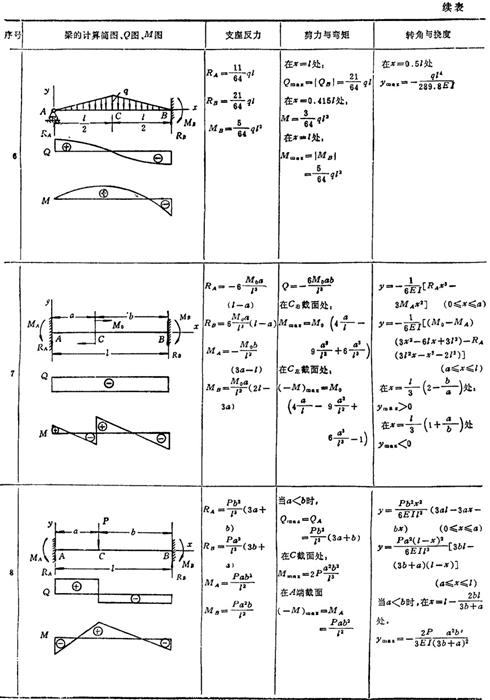
③用积分法计算梁的挠度、转角，除了要求列出梁各段的弯矩方程外，还需正确列出足够的边界条件来确定积分常数，几种常见梁的边界条件见表1．3－10。

表1．3－10 几种常见梁的边界条件

1．2．2 组合变形杆件的强度计算公式

杆件在外力作用下同时产生两种或两种以上的基本变形的情况，称为组合变形。工程上最为常见的有斜弯曲(双向弯曲的组合)、拉(压)弯组合和弯扭组合等。组合变形杆件的强度计算公式见表1．3－12。

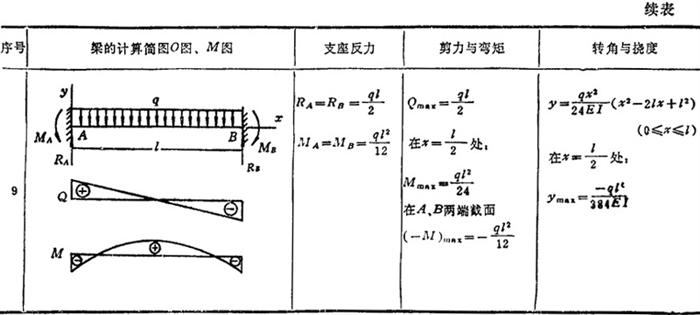
表1．3－11 梁的Q图、M图及变形计算公式

表1．3－12 组合变形杆件的强度计算公式

1．2．3 变形(位移)计算的能量法

利用能量法计算杆件乃至结构的指定点位移(线位移、角位移)是应用广泛，方便有效的方法。

在外力作用下，弹性体因其变形而贮存的能量，称为弹性变形能，它在数值上等于外力所做的功，其计算公式如表1．3－13所示。表1．3－14列出计算杆件变形(位移)能量的莫尔积分法和图形互乘法。

表1．3－13 弹性变形能计算公式

注①裄架的变形能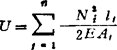(n为桁架的杆数)。②由剪力Q引起的变形能，一般情况下，可以忽略。式中系数k与截面形状有关：矩形，k=1．2；圆形，k=1．1；工字形，k=2～2．3。

表1．3－14 莫尔积分法和图形互乘法

注：用莫尔积分法求细长梁的挠度和转角时，可略去剪力(Q)项，用莫尔积分法求刚架定点位移时，可略去剪力(Q)项和轴力(N)项。

表1．3－15 简单图形的面积和形心坐标

1．2．4 超静定问题的解法

(1)基本概念

受力杆件或结构的约束反力和内力仅用静力学平衡方程即可求解的问题，称为静定问题。

当受力杆件或结构的约束反力和内力数多于独立的静力学平衡方程数时，仅用静力学平衡方程不再能求出全部未知力，此类问题即为超静定问题。出于工程上的需要(如提高杆件的强度、刚度或工作的要求)，在静定结构上增添了新的“多余”约束(它们从维持平衡而言，是多余的)，从而增加了多余未知力。显然，多余未知力的个数即是超静定次数，亦即为求解该超静定问题需要增加的补充方程个数。

解超静定问题时常以力为未知数，这类方法称为力法。用力法求解超静定问题的步骤如下：

①判断是否为超静定问题，是几次超静定问题。

②选定并解除多余约束，代之以多余未知力，即得到与原超静定结构完全相当的静定系统。‘相当’的必要条件是在多余未知力处的位移应与超静定结构相应位置的位移相等。

③列出相当系统中多余未知力作用点的位移条件。并将各项位移表示为力的函数，即得到求解所需要的补充方程。

④解补充方程(或补充方程组)，即求得多余未知力。

⑤利用静力学平衡方程求出其他约束反力，然后，如静定结构一样地进行强度、刚度计算。

对于高次超静定结构，比如n次超静定向题的求解，则需求解n个位移条件组成的联立方程，即力法正则方程〔4〕。

(2)超静定梁的计算公式

利用力法求得简单超静定梁的支座反力、最大弯矩和挠度、转角如表1．3－16所示。

表1．3－16 简单超静定梁的计算公式