杆件的动应力强度计算

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第133页（2077字）

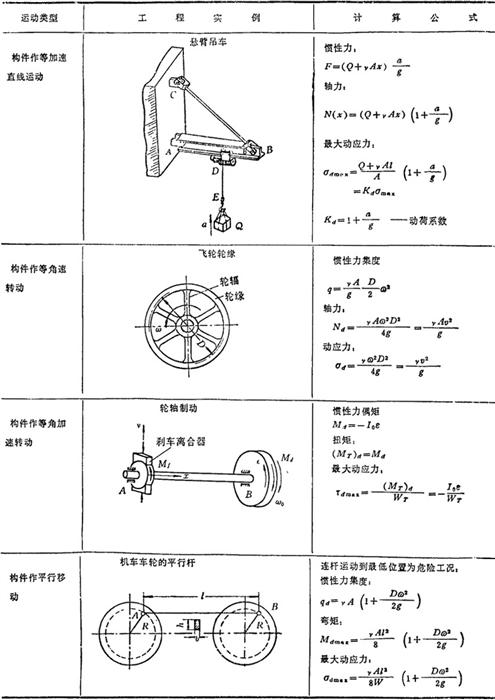
1．5．1 惯性力问题

杆件在一般加速度运动时，由惯性力引起杆件的动应力，用“动静法”求解。在此情况下，材料的机械性质的变化可忽略不计，强度计算与静载荷问题相同，因此，主要工作是求出杆件的最大动应力。

表1．3－24 几种由惯性力引起的动应力

1．5．2 冲击应力的计算

运动物体在极短的时间加于杆件的载荷，称为冲击载荷，由于时间极短，速度变化很大，加速度很难计算，故不能应用“动静法”求解，而是采用能量法近似求解。

(1)冲击应力的计算方法

基本假设：1．冲击物变形很小，可视为刚体；2．被冲击物质量比冲击物质量小得多；3．略去冲击过程的能量损耗。

基本方程：T+V=U_d

式中 T为冲击过程中冲击物减少的动能；V为冲击过程中冲击物减少的位能；U_d为冲击过程中被冲击物增加的弹性变形能。

计算公式： σd=Kdσ_st；

σdmax=K_d(σst)_max≤〔σ〕 (1．3－23)

式中 σ_d为冲击应力；σ_st为相应的静应力(将冲击物重量作为静载荷作用在冲击点处，所求得的应力)；Kd为动荷系数(不同的冲击方式，有不同的动荷系数)。

求冲击应力，实际上是相应的静应力和动荷系数的乘积。

铅垂冲击动荷系数：已知冲击物重量Q和自由下落高度H时，则

式中 △_st是Q作为冲击点的静载荷求得的冲击点沿冲击方向的静位移。

已知冲击物在冲击开始的速度u时，则

式中 g为重力加速度。

已知冲击物在冲击开始时的初动能T₀以及被冲击物的静荷变形能U时，应为

动荷系数在下列条件下可取近似值：

若被冲击物的质量较大，不能忽略，其质量比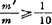时在动荷系数中要考虑修正系数a，即

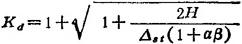
式中 a为修正系数； ，为被冲击物和冲击物的质量比。

水平冲击动荷系数：已知冲击物重量Q和水平冲击速度v时，

式中 △_st是Q作为水平方向的静载荷作用于冲击点处，在该处产生的静位移。

(2)几种典型冲击问题的动应力，见表1．3－25．

表1．3－25 几种典型冲击问题的动应力

1．5．3 振动应力的计算

物体在其静平衡位置附近产生变形，作周期性运动，即为振动。图1．3－25所表示为悬臂梁的振动，其最大动位移为

图1．3－25 悬臂梁的振动

式中 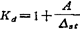，为动荷系数；A为振幅；△_st为静位移。

由上式知，计算振动应力的关键是求动荷系数K_d。△_st的计算可参见前面有关部分。振幅的计算

式中 H为干扰力的最大值：β为放大系数。

式中 n为阻尼系数；ω为干扰力频率；ω₀为杆件的固有频率。

对一个自由度的杆的纵向振动

对一个自由度的梁的横向振动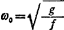

对一个自由度圆轴的扭转振动

一个自由度杆件的纵向或横向振动，其动荷系数K_d由上述关系可推出如下形式：