弹性结构的动力分析

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第193页（3150字）

当载荷随时间变化时，节点位移也必将随时间变化，此时应考虑结构质量的惯性力作用以及结构的阻尼特性。根据达朗贝尔原理，将单元惯性力作为体力的一部分，并考虑随速度变化的阻尼力，弹性结构的运动方程可写成：

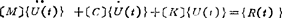(1．3－83)

式中 〔M〕总体质量矩阵，由单元质量矩阵〔m〕组集而成；〔C〕总体阻尼矩阵，对于瑞利线性阻尼为：

〔C〕=α〔M〕+β〔K〕 (1．3－84)

系数α和β可以通过测定结构自由振动的衰减率求得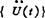；，｛U(t)｝和｛U(t)｝分别为总体节点加速度矢量、总体节点速度矢量和总体节点位移矢量。

单元质量矩阵〔m〕的算法有两种：

①一致质量矩阵：

式中 ρ为材料质量密度；〔H〕为单元插值矩阵。单元一致质量矩阵是满矩阵，组集成的总体质量矩阵〔M〕是和总刚矩阵〔K〕一样的带状矩阵，占用很大的存贮量，求解运动方程运算机时多。实际表明，采用一致质量矩阵并没有带来明显的精度提高。一般通用有限元程序都采用集中质量矩阵。

②集中质量矩阵：

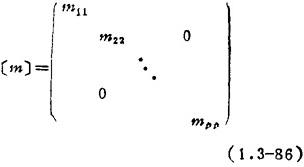
它将单元质量ρV_n(V_n单元体积、ρ材料质量密度)近似地分配到单元各节点上，形成对角矩阵。由单元集中质量矩阵组集成的总体质量矩阵也是对角矩阵，可以显着节省存贮量和求解运动方程的机时，

3．5．1 弹性结构的无阻尼自由振动

将运动方程中｛R(t)｝=0和〔C〕=0，得到弹性结构的无阻尼自由振动方程：

(1．3－87)

它是常系数线性齐次常微分方程组，其解为如下形式的简谐运动：

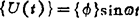
式中 ｛Φ｝是结构的振型；ω是结构的固有频率，将上式代入自由振动方程，消去公共因子sinωt得：

(〔K〕－ω²〔M〕)｛Φ｝=0

求解自由振动方程问题化为寻找满足上式的ω²值和非零矢量｛Φ｝。这样的问题在数学中你为广义特征值问题。令λ=ω²，λ和｛Φ｝分别称为特征值和特征矢量。上述齐次线性方程组要有｛Φ｝的非零解，必须是它的系数行列式等于零，即

|〔K〕－λ〔M〕|=0

在弹性结构动力分析中，〔K〕和〔M〕矩阵的阶数n很大。上述行列式展开成λ的n次代数方程式，要直接求解n个广义特征值λ₁，λ₂、…λ_n，显然是不可能的，工程中通常只要求得到若干低频的特征值和特征矢量。现已研究出多种有效的数值近似解法，并编制成标准程序模块。在通用有限元程序中常见的算法有：行列式搜索法(全内存求解)和子空间迭代法(〔N〕和〔M〕分块内外存交换求解)。

3．5．2 弹性结构动力响应计算

在给定初始条件下如何求解运动方程，常用的有两类解法，直接积分法和振型迭加法，

(1)直接积分法

对运动方程按时间步直接进行数值积分求解。它在离散的时步点上要求满足运动方程，而在时步内假定位移、速度和加速度按某种规律变化。不同算法采用不同变化规律。

①中心差分法。t时刻节点速度和加速度的中心差分表达式为

代入运动方程得

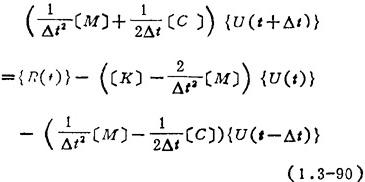
由上式求解｛U(t+△t)｝。一般初始条件给定｛U(0)｝和，而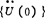由t=0时刻运动方程求出，再由(1，3－88)和(1．3－89)式联解得：

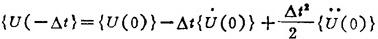
循环运用方程(1．3－90)、(1．3－88)和(1．3－89)，可以依次求得各个时间步的节点位移、速度和加速度。中心差分法是条件稳定的。稳定性要求时步长△t小于等于极限时步长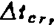即

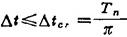
其中T_n是结构自由振动的最小周期。

②纽马克Newmark法。它的积分格式是线性加速度法的推广，采用的假定是：

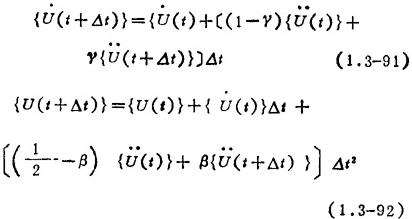
其中γ和β是任选的参数。当γ≥0．5和β≥(2γ+1)²／16时，纽马克法是无条件稳定的。对于线性问题，较好的参数选择是γ=0．5和β=0．25，

由(1．3－91)、(1．3－92)式可导出用｛U(t+△t)｝为基本未知量表示的t+△t时刻速度矢量和加速度矢量，再代入t+△t时刻的运动方程，得

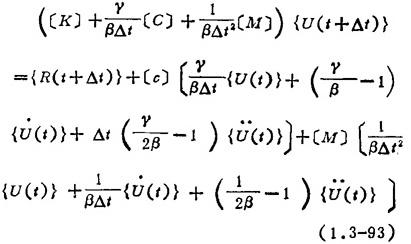
从t=0时刻开始求解。将给定的初始条件｛U(0)｝和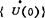代入运动方程得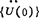。循环运用方程(1．3－93)、(1．3－91)和(1．3－92)，可以依次求得各个时间步的节点位移，速度和加速度。

直接积分法还有许多算法，如威尔逊Wilson－θ法，四阶龙格——库塔Runge－Kutta法等。

(2)振型迭加法

先计算部分低阶结构振型｛Φ｝₁、｛Φ｝₂、…｛Φ｝_m，(m《n，n是总刚矩阵阶数)，用这些少量的结构振型的线性组合近似表示总体位移矢量｛U(t)｝，即

｛U(t)｝=〔Φ〕｛x(t)｝ (1．3－94)

式中 ｛x(t)｝是与时间有关的m阶矢量，它的各个分量x₁(t)，x₂(t)，…x_m(t)称为广义位移；〔Φ〕=〔Φ₁Φ₂…Φ_m〕，为振型矩阵，

将(1．3－94)式代入运动方程，再在等式两端左乘〔Φ〕^T，得++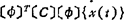〔Φ〕T〔K〕〔Φ〕｛x(t)｝=〔Φ〕^T｛R(t)｝

考虑到振型的正交性质，即

〔Φ〕^T〔M〕〔Φ〕=〔I〕

〔Φ〕^T〔K〕〔Φ〕=〔Ω〕

式中 〔I〕为m×m单位矩阵；

wl(i=1，2，…m)，为结构固有频率。

上式可写成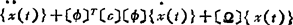=σ〕T｛R(t)｝

若采用瑞利阻尼〔C〕=α〔M〕+β〔K〕，则

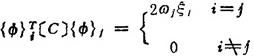
此时上式化成m个互不耦合的二阶常微分方程：

x_l(t)+2ω_lξlx_l(t)+ω2ix_l(t)=γ_l(t)

i=1，2，…m (1．3－95)

式中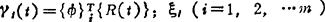称为振型阻尼比。

该方程相当于一个单自由度系统的振动方程，比较容易求解。求得广义位移x₁(t)，x₂(t)，…x_m(t)后，再代回(1．3－94)式得到｛U(t)｝。按各时间步t=0_，△t_，2△t，…依次求得结构的动力响应。

由于在振型迭加法中略去高频响应，故适用于低频载荷引起的结构动力响应分析。对于冲击等动力问题，激发振型较多，只要计算较短时间的动力响应，通常以采用直接积分法为宜。