辐射换热过程

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第229页（2586字）

辐射换热过程包括辐射传热及辐射放热两种基本传热过程。

2．4．1 热辐射的基本定律

热辐射的定律有多条，其中最重要的是斯蒂芬—玻尔茨曼定律和克希荷夫定律。

(1)斯蒂芬—玻尔茨曼定律

物体牺牲本身的热能，在单位时间内通过单位表面积所放射出去的辐射能量，称作该物体的辐射力，用E表示，单位是W／m²。

黑体的辐射力与物体表面的绝对温度的4次方成正比例，可表示为：

上式即斯蒂芬—玻尔茨曼定律的表达式。其中，E₀为黑体的辐射力；σ₀=5．67×10－⁸W／(m²·K4)，为黑体的斯蒂芬－玻尔茨曼常数；C₀=5．67W／(m²·K⁶)，为黑体的辐射系数。

不同物体具有一共性：任何物体，如果它吸收辐射能的能力越大，其放射辐射能的能力也越大：反之，亦然。黑体的吸收能力最大，故其放射能力也最大；其它物体(非黑体)吸收能力较小，故其放射能力也较小。非黑体的辐射力E与同温度的黑体的辐射力之比，称作该物体的黑度：

实际物体的黑度，0＜ε＜1。常用材料的表面黑度见表1．4－23。

表1．4－23 常用材料的表面黑度

由(1．4－66)式可得实际物体的辐射力：

(2)克希荷夫定律

前面提到的：“任何物体，若其吸收辐射能的能力强，则其放射辐射能的能力也强；反之亦然。”这实际上就是克希荷夫定律。该定律可简单表达如下：

a=ε (1．4－68)

即一物体的吸收率和黑度在数值上相等。

严格地讲，只有对黑体及灰体，a=ε是完全正确的；而对于有色体，只有当它被等温的黑体包围时，才是正确的。不过，对于单色吸收率和单色黑度，则任何物体在任何情况下，下式都是成立的：

a₁=ε_λ (1．4－69)

2．4．2 固体表面间的辐射传热过程

辐射换热过程中有一特点：不但高温物体传热给低温物体，而且低温物体也同时传热给高温物体。不过前者多于后者。所以，总的效果是高温物体传热给低温物体。

多数工程材料近似于灰体，故可当作灰体计算，两灰体表面间的辐射传热量Q₁－₂，即指总的效果，可用下式计算：

式中 A₁、A₂分别为表面1、2的表面积，m²；T₁，T₂分别为表面1、2的绝对温度，K；ε₁、ε₂分别为表面1、2的黑度；φ_1－2为表面1对表面2的角系数。

由(1．4－70)式可见，角系数φ_1－2值的确定是计算辐射传热量Q_1－2的关键。角系数的确定方法有多种，常用的有：

①积分法。此法只适用于几何条件不很复杂的情况。可由下述基础公式积分得到角系数：

式中 r为微元面积dA₁和dA₂之间的距离；φ₁，φ₂是dA₁与dA₂的连结线分别与dA₁、dA₂的法线之间的夹角。

②代数法。此法是基于表面间辐射传热的互换性原理、完整性原理和分解性原理。

互换性原理：任何两表面之间进行辐射传热时，必符合下列关系式：

A1φ_1－2=A₂φ_2－1 (1．4－72)

完整性原理：在一个由若干平面(或凸面)组成的封闭辐射系统中，从一个面放射和反射出去的射线(即有效辐射)以不同的百分数投射到其它各表面上，各百分数之和必等于100%，

应用上述两种原理就可对封闭辐射系统写出很多代数方程式，求解这些联立方程式即可确定有关的角系数的值。

分解性原理：当两表面A₁和A₂进行辐射传热时，如单独把A₁表面分解为A₃和A₄，可写出：

A₁φ_1－2=A₃φ_3－2+A₄φ_4－2

若单独把A₂分解成为A₅和A₆，则也可写出：

A₁φ₁－₂=A₁φ₁－5+A₁φ_1－6

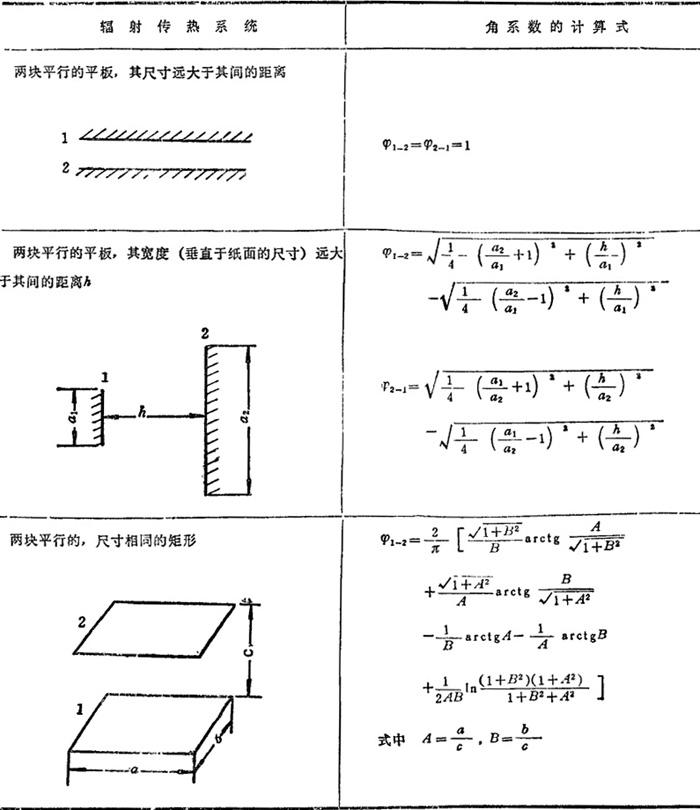
③利用已有公式(或线图)。实际上，为了方便起见，对不同相对位置的两表面间的角系数已由理论导出计算式，并画成线图。表1．4－24列出三例：

表1．4－24 某些辐射系统的角系数

2．4．3 气体与固体表面间的辐射放热过程

单原子气体及对称型双原子气体的热辐射可以忽略不计，它们可被视为透明体。但是，非对称型双原子气体、三原子气体及多原子气体，都具有一定的吸收及放射辐射能的能力，它们的热辐射不可忽略不计。与固体相比，气体的热辐射具有很多特殊的性质，因而气体与固体壁面之间的辐射放热往往采用半理论半经验的公式进行计算，例如在计算燃烧气体与气缸壁之间的辐射放热量时，常采用下述公式：

式中 ε_w为气缸壁表面的黑度；T_g为燃烧气体的绝对温度，K；T_w为气缸壁表面的绝对温度，K；A_u为气缸壁内表面积，m²_；ε_g及a_g分别是燃气的黑度及吸收率，其取值方法可参看有关资料。