任意角的三角函数
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第31页(2001字)
1.任意角的三角函数定义
设α是一个任意大小的角.角α的终边上任意一点P的坐标是(x,y),它与原点的距离是r(r>0),那么角α的正弦、余弦、正切、余切、正割、余割分别是
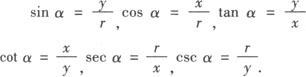
2.正弦、余弦、正切、余切、正割、余割分别可看成是从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,这六个函数统称为三角函数.
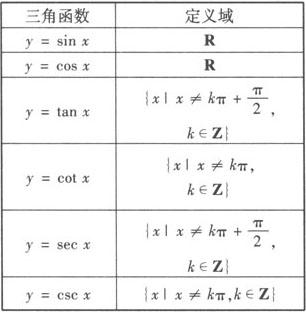
注 确定三角函数的定义域时,主要应抓住分母为零时比值无意义这一关键,当且仅当角的终边在坐标轴上时,点P的坐标中必有一个为0.
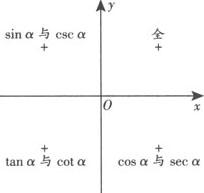
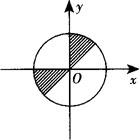
3.三角函数值的符号
各三角函数值在每个象限的符号如图(各象限注明的函数为正,其余为负).
例1 已知sinα>sinβ,则下列命题成立的为( ).
A.若α、β是第一象限角,则cosα>cosβ
B.若α、β是第二象限角,则tanα>tanβ
C.若α、β是第三象限角,则cosα>cosβ
D.若α、β是第四象限角,则tanα>tanβ
答案 D.
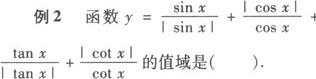
A.{—2、4}
B.{—2、0、4}
C.{—2、0、2、4}
D.{—4、—2、0、2、4}
答案 B.
例3 已知点P(sinα—cosα,tanα)在第一象限,则在[0,2π)内α的取值范围( ).
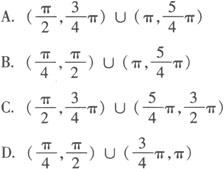
分析 在同一直角坐标系中作出单位圆和直线y=x,由已知有sinα>cosα,故角α的终边应该落在直线y=x的上方半个圆内.
又∵tanα>0,角α的终边应该落在第Ⅰ、第Ⅲ两个象限内,如图,可知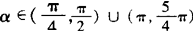 .应选B.
.应选B.
例4 (1)角α的终边上一个点P(4t,—3t)(t≠0),求2sinα+cosα的值.
(2)已知角β的终边在直线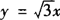 上,用三角函数定义,求sinβ和cotβ的值.
上,用三角函数定义,求sinβ和cotβ的值.
分析 (1)由题目特点,可考虑利用三角函数的定义求解.
解 据题意,有x=4t,y=—3t,
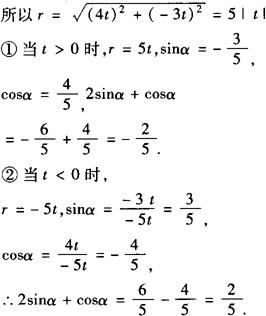
(2)设P(a,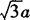 )(a≠0)是角β终边y=
)(a≠0)是角β终边y=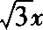 上一点,则
上一点,则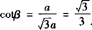 .
.
若a<0,则β是第三角限角,r=—2a,
此时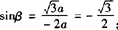 ;
;
若a>0,则β是第一角限角,r=2a,
此时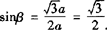 .
.
评注 本例(1)(2)中参数t和a都是不为零的实数,所以应对它们分类讨论,这是不应忽略的.
例5 已知一扇形的中心角是α,所在圆的半径是R.
(1)若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积.
(2)若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积.
解 (1)设弧长为l,弓形面积为S弓,
