异面直线的判定定理
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第88页(444字)
过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.
例 如图,已知α∩β=l,A∈l,B∈l,且 ,
, 求证:AE和BF是异面直线.
求证:AE和BF是异面直线.

策略 证明两条直线是异面直线,通常用反证法.
证明 假设AE和BF共面,因为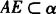 ,B∈α,且
,B∈α,且 ,所以过AE及点B有且只有一个平面α,因此
,所以过AE及点B有且只有一个平面α,因此 ,这就与
,这就与 且α∩β=l相矛盾,故AE和BF是异面直线.
且α∩β=l相矛盾,故AE和BF是异面直线.
点评 用反证法证a、b是异面直线,有时要否定a∥b及a∩b=A两种情况,本例是直接否定a、b共面,反证法是一种十分重要的方法,在立体几何中有着广泛的应用,熟练地掌握和运用反证法是学习立体几何的必备基础之一,反证法证明的一般步骤为(1)反设;(2)归谬;(3)结论.
上一篇:共点、共线、共面问题
下一篇:等角定理的推论