直线与平面的位置关系

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第90页（968字）

一条直线与一个平面的位置关系有且只有以下三种：

(1)直线在平面内——有无数个公共点；

(2)直线和平面相交——有且只有一个公共点；

(3)直线和平面平行——没有公共点．

我们把直线和平面相交或平行的情况统称为直线在平面外．

【说明】 下图是表示三种位置关系的图形，直线a与平面α相交于点A，记作a∩α=A，直线a与平面α平行，记作a∥α，直线a在平面α外，记作．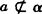

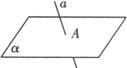
例 已知一条直线与一个平面平行，求证经过这个平面内的一点与这条直线平行的直线必在这个平面内．

已知：直线a∥平面α，点A∈α，点A∈直线b，且a∥b．

求证：．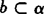

策略 直线在平面内的判定方法；(1)公理1；(2)直线与平面位置关系共三种，排除其中两种(相交、平行)即为第三种．

证明 反证法

假设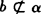内，

∵A∈α，A∈b，∴b和α相交，

∵a∥α，A∈α，

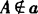∴，则过点A和a存在一个平面β，即A∈β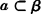，，在β内，过A可作直线b′，使a∥b′且A∈b′．

又∵a∥b，∴b′∥b，与b∩b′=A矛盾，

∴．

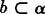点评 此题结论可作为直线在平面内的又一种判定方法．