正多面体的种类
书籍：高中数理化公式定理大全
出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第100页（1491字）
正多面体只能有5种，用正三角形做面的正四面体、正八面体、正二十面体，用正方形做面的正六面体，用正五边形做面的正十二面体．
例1 如下图所示，三棱锥P—ABC中，PA=PC，∠APC=∠ACB=90°，∠BAC= 30°，且平面PAC⊥平面ABC
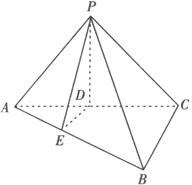
(1)求证：平面PAC⊥平面PBC．
(2)求二面角P—AB—C的正弦值．
(3)若PA=2，求三棱锥P—ABC的体积．
解 (1)证明 ∵平面PAC⊥平面ABC，面PAC∩面ABC=AC，又BC⊥AC，
∴BC⊥平面APC，
又∵
，∴平面PAC⊥平面PBC．
(2)过P作PD⊥AC于D，则PD⊥平面ABC，过D作DE⊥AB于E，连结PE．
∵面PAC⊥面ABC，∴PD⊥面ABC．
由三垂线定理知：∴PE⊥AB．
∴∠PED为二面角P—AB—C的平面角．
设PA=PC=a，∵∠APC=90°，
例2 已知正四棱锥P—ABCD的底面边长和各侧棱长都是13，M、N分别是PA、BD上的点，且PM∶MA=BN∶ND=5∶8．
(1)求证：MN∥平面PBC．
(2)求直线MN与平面ABCD所成角的正弦值．
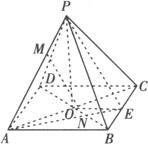
解 (1)证明 如图所示，连AN并延长交BC于E，连结PE．
∵AD∥BC，
∴△AND～△BNE，
∴EN∶AN=BN∶ND．
又BN∶ND=PM∶MA，
∴EN∶AN=PM∶MA，
∴MN∥PE，又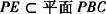
．
∴MN∥平面PBC．
(2)由(1)知MN∥PE，
∴PE与平面ABCD所成的角即MN与平面AC所成的角．
设底面中心为O，连结PO，则PO⊥面AC，连结OE，则∠PEO为PE与底面AC所成角．
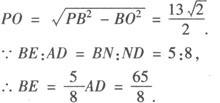
又在△PBE中，由余弦定理得：
