机车起动的两种理想模式
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第206页(1768字)
1.以恒定的功率P起动(从静止开始运动)和行驶,设机车质量为m,所受阻力f大小不变,由P=F及牛顿第二定律得牵引力 (P不变),
(P不变), ,分析可知,开始起动v很小,F很大,a很大,且a(F)与v同向,v用↑表示增大)—F↓(用“↓”表示减小)—a↓—v↑.当F=f,a=0时,速度达到最大
,分析可知,开始起动v很小,F很大,a很大,且a(F)与v同向,v用↑表示增大)—F↓(用“↓”表示减小)—a↓—v↑.当F=f,a=0时,速度达到最大 .机车的运动分两个阶段:第阶段做加速度逐渐减小的加速运动(牵引力逐渐减小);第二阶段做匀速运动,两个阶段的连结点处:F=f,a=0,速度大小为v↓(m
.机车的运动分两个阶段:第阶段做加速度逐渐减小的加速运动(牵引力逐渐减小);第二阶段做匀速运动,两个阶段的连结点处:F=f,a=0,速度大小为v↓(m ,因牵引力大小在变化而功率恒定,故可用公式W=Pt求牵引力所做之功,(在加速运动阶段能量关系为:Pt—fs=1/2mv2)克服阻力所做之功为W′=fs,其速度图象如图所示.
,因牵引力大小在变化而功率恒定,故可用公式W=Pt求牵引力所做之功,(在加速运动阶段能量关系为:Pt—fs=1/2mv2)克服阻力所做之功为W′=fs,其速度图象如图所示.

2.机车以恒定加速度起动直到以额定功率P额行驶.
由基本公式P=F.v和 分析可知:牵引力F=f+ma.开始,a和f不变,F也不变,v很小,P很小,vP↑〔P=(f+ma)at〕.当功率增大到额定功率时,速度增大到
分析可知:牵引力F=f+ma.开始,a和f不变,F也不变,v很小,P很小,vP↑〔P=(f+ma)at〕.当功率增大到额定功率时,速度增大到 .此后功率保持P↓(额不变,vF↓—a↓—v↑;当F=f时,a=0,速度达最大
.此后功率保持P↓(额不变,vF↓—a↓—v↑;当F=f时,a=0,速度达最大 .
.
机车的运动分三个阶段:首先是匀加速运动阶段(此阶段F、f、a都不变,v及P随时间均匀增加,可用W=Fs和W′=fs求牵引力所做功和克服阻力所做的功,其末态情况是:P=P↓(额, );接着做加速度减小的加速运动(此阶段,功率P额不变,f不变,a↓,F↓,v末态情况是:F=f,a=0,v↓(m=
);接着做加速度减小的加速运动(此阶段,功率P额不变,f不变,a↓,F↓,v末态情况是:F=f,a=0,v↓(m= );最后匀速运动(F=f,P=P额,vm=
);最后匀速运动(F=f,P=P额,vm= ),其速度图象如图所示.
),其速度图象如图所示.

例 汽车发动机的额定功率为Pm=60kW,汽车质量为m=5t,运动时与地面的摩擦因数为μ=0.1.求:
(1)汽车所能达到的最大速度vm.
(2)若汽车以a=0.5m/s2的加速度由静止开始做匀加速直线运动,这一过程能维持多长时间?(g=10m/s2)
(3)当速度v1=4m/s时,汽车的加速度a1是多大?功率P1是多大?
(4)当速度v2=10m/s时,汽车的加速度a2是多大?功率P2是多大?
分析 准确分析汽车的运动状态是解题的关键.
解 (1)当汽车达到最大速度vm时,a=0,牵引力F等于阻力f,f=μmg,再由Pm=F·vm得最大速度大小为

(2)汽车从静止开始匀加速启动,牵引力F恒定且由
F—f=ma
得 F=f+ma=μmg+ma.
由于速度不断增大,因此发动机功率P也不断增大(因P=Fv∝v),当功率增至额定功率Pm时,匀加速运动结束,其匀加速运动阶段的最大速度为

故可知加速运动维持的时间为

(3)由于速度v1=4m/s
(4)由于速度v2=10m/s>v′且v2
 ,加速度
,加速度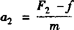 =
= .
.